부스트 캠프 ai tech 1주 3일차 Ai Math (6)

---

6. 베이즈 통계학

• 하나의 사건에서 믿음의 정도를 확률로 나타내는 베이즈 확률론에 기반한 통계학 이론
• 쉽게 말하면 아직 일어나지 않은 사건이 일어날 확률에 대한 계산을 하는 학문

6.0 조건부 확률

• 조건부확률 $P(A|B)$
  특정사건 $B$가 일어난 상황에서 사건 $A$가 일어날 확률이다. 아래와 같이 나타낼 수 있다.

  $A$와 $B$가 동시에 일어날 확률 = $B$가 일어날 확률 * $B$일어난 상황에서 $A$가 일어날 확률
  $$
  P(A\cap B) = P(B), P(A|B) = P(A), P(B|A)
  $$
  $$
  P(B|A) = \frac{P(A\cap B)}{P(A)} = P(B) \frac{P(A|B)}{P(A)}
  $$

6.1 베이즈 정리

• $D$ : 데이터

• $\theta$ : 측정하고싶은 파라미터

• 조건부 확률 $P(\theta|D)$는 사후확률이라고 부른다

• 조건부 확률 $P(D|\theta)$는 가능도(likehood, 우도)라고 부른다

• $P(\theta)$ 는 사전확률이라고 부른다

• 베이즈 정리는 아래와 같이 나타내며 이식으로 부터 우리는 사후확률과 가능도는 비례하는 관계임을 알 수 있다
  $$
  P(\theta|D) = P(\theta) \frac{P(D|\theta)}{P(D)}
  $$

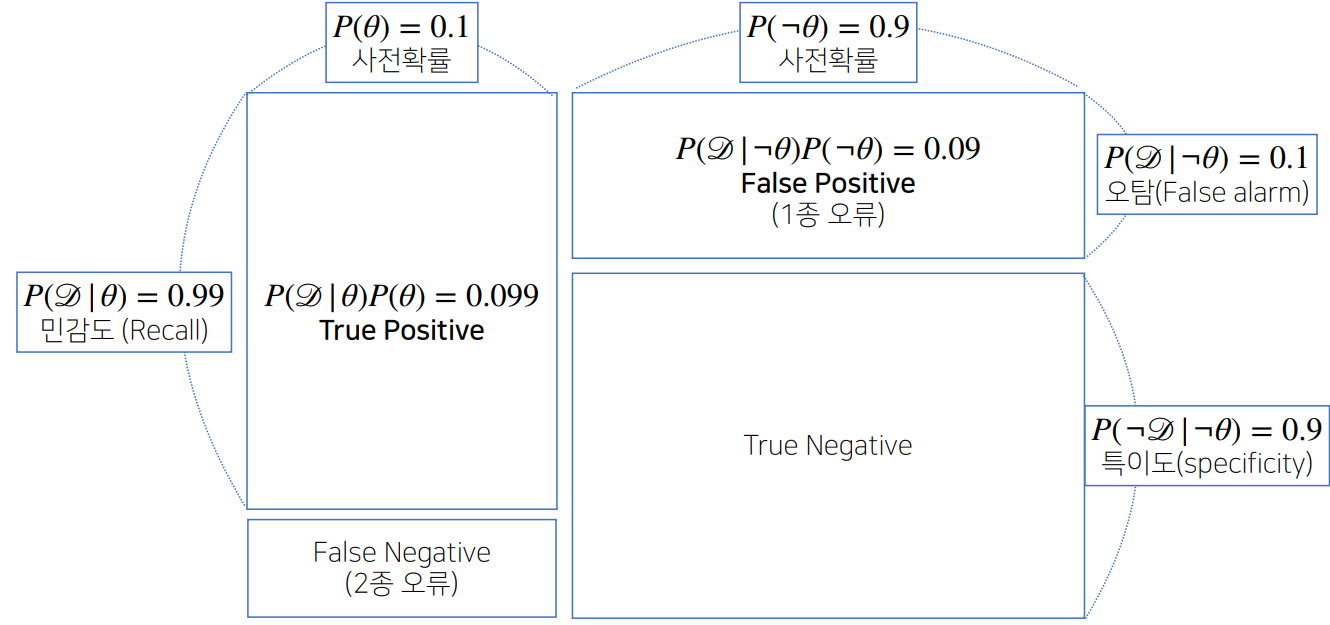
• 조건부 확률의 시각화

  • 정밀도(Precision) : 모델이 True라고 분류한 것들 중에서 실제 True인 것의 비율
  • 재현율(Recall) : 실제 True인 것 중에서 모델이 True라고 예측한 것의 비율
  • 정확도(Accuracy) : 올바르게 예측한 정도
    $$
    Precision = \frac{TP}{TP+FP}
    $$
    $$
    Recall = \frac{TP}{TP+FN}
    $$
    $$
    Accruacy = \frac{TP + TN}{TP+FN+FP+TN}
    $$

• 새로운 데이터가 들어왔을때 앞서 계산한 사후확률을 사전확률로 사용하여 새로운 사후확률로 갱신할 수 있다
  $$
  P^{\prime}(\theta|D) = P(\theta|D) \frac{P(D|\theta)}{P(D)}
  $$

• 조건부 확률은 일어나지 않은 일에 대해 유용한 통계적 해석을 제공하지만 인과관계를 추론할때는 함부로 사용해서는 안된다

• robust한 모델을 위해서는 인과관계를 생각할 필요가 있다