부스트 캠프 ai tech 1주 3일차 Ai Math (7)

---

7. CNN

• 합성곱을 이용한 신경망

7.1 Convolution 연산

• 신호(signal)를 커널을 이용해서 국소적으로 증폭 또는 감소시키는 연산을 말한다

• CNN 에서 하는 연산은 엄밀하게 말하면 Cross Correlation 연산이다

  • Cross Correlation
    $$
    [f*g](x) = \int_{\mathbb{R}}f(z)g(x+z)\operatorname{d}z
    $$
  • Convolution 연산
    $$
    [f*g](x) = \int_{\mathbb{R}}f(z)g(x-z)\operatorname{d}z
    $$

• 다양한 차원에서 연산이 가능하다
  $$
  \begin{aligned}
  &1D \quad [f*g](i) = \sum_{p=1}^{d}f(p)g(i+p)\\
  &2D \quad [f*g](i,j) = \sum_{p,q}f(p,q)g(i+p,j+q)\\
  &3D \quad [f*g](i,j,k) = \sum_{p,q,r}f(p)g(i+p,j+q,k+r)
  \end{aligned}
  $$

7.1 2D Convolution 연산

• 2차원 convolution 연산은 커널을 input위에서 움직여가면서 선형모델과 합성함수가 적용되는 구조이다.

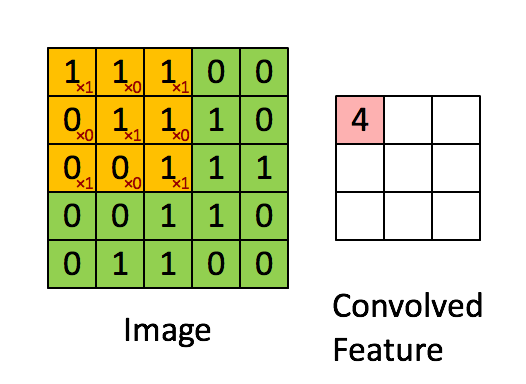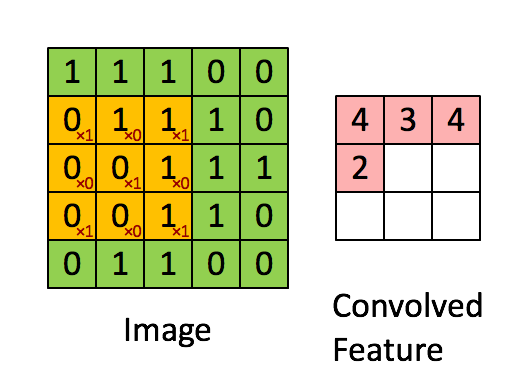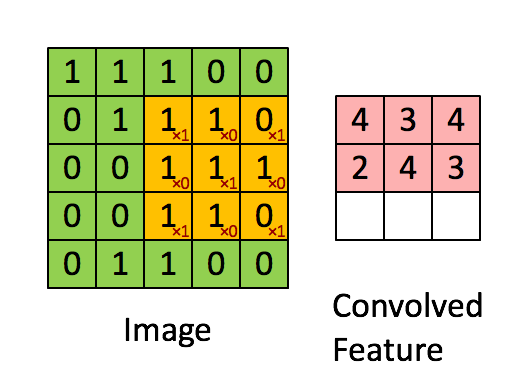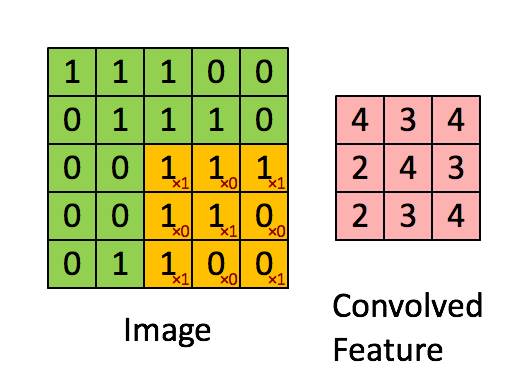
• 출력크기는 아래와 같이 계산된다

  • $H, W$ : 입력크기
  • $K_{h}, K_{w}$ : 커널의 크기
  • $O_{h}, O_{w}$ : 출력의 크기
    $$
    O_{h} = H-K_{h}+1\\
    O_{w} = W-K_{w}+1
    $$

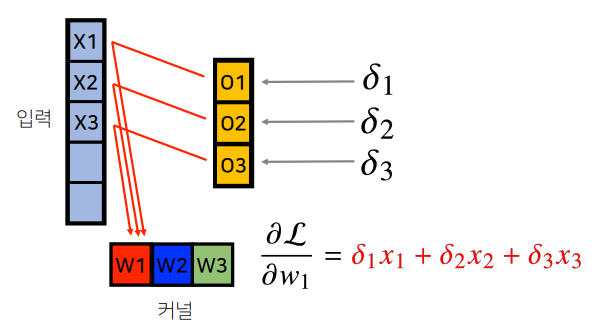
7.2 Convolution 연산의 Backpropagation

• Convolution 연산의 역전파도 결국에는 선형연산이 여러번 적용된 형태이기 때문에 계산할때 각 커널의 들어오는 모든 gradient를 더하면 된다

$$
\frac{\partial \mathcal{L}}{\partial w_{i}} = \sum_{j} \delta_{j} x_{i+j-1}
$$