FCOS: Fully Convolutional One-Stage Object Detection
논문 링크 : https://arxiv.org/pdf/1904.01355.pdf
첫 논문 리뷰로 YoloX 등의 고성능 Anchor Free 모델에 응용되는 OB 모델인 FCOS에 대해서 리뷰를 진행하겠습니다.
간단 요약
Anchor Free기반의 Object Detection Model- Semantic Segmentation과 비슷하게 Pixel 단위의 예측을 통하여 Object Detection(OB)을 진행
- FPN + Multi head Branch를 이용하여 성능 UP
- Center-ness을 이용하여 좀 더 정확성을 끌어올림
Anchor Based Model의 한계
본 논문에서 지금 까지의 OB모델들은 Anchor Box Base로 좋은 성능을 내어왔지만 다음과 같은 단점이 존재한다고 서술한다
- Anchor Box 또한 Hyper Parameter로써 성능에 매우 큰 영향을 미치기 때문에 조심스러운 튜닝이 필요하다
- 조심스럽게 튜닝을 마쳐도 고정된 Anchor Box의 크기와 차이가 많이 나면 효과적으로 학습하지 못한다
- 높은 Recall 성능을 얻기 위해서는 촘촘한 Anchor Box가 필요하다. 수많은 Anchor Box들은 많은 Negetive Sample을 생성하며 Positive와의 균형이 깨어져서 Imbalance를 야기한다
- Anchor Box와 Ground Truth(GT)와의 IoU 계산에서 많은 코스트가 필요하다
이를 통하여 본 논문에서는 이런 단점을 해결하기 위해 Anchor Free Object Detection Model인 FCOS를 제안하였다
논문에서 제안한 Point
0. 사전 설정
- 먼저 Layer $i$ 의 Feature Map을 $F_{i}$ 라고 하고, input 이미지의 GT를 $B_i = (x^{i}_{0}, y^{i}_{0}, x^{i}_{1}, y^{i}_{1}, c^{i})$ 라고 설정한다.
- $(x^{i}_{0}, y^{i}_{0})$ : left-top
- $(x^{i}_{1}, y^{i}_{1})$ : right-bottom
- $c^{i}$ : class
- Feature Map에서의 위치 좌표 $(x, y)$ 는 실제 이미지에서 다음의 좌표와 대응된다.
- (xs, ys)로만 표현할 경우 오차의 범위가 너무 커지기 때문에 stride의 절반을 더해주어서 보상한다
- $s$ : size of stride
$$
([\frac{s}{2}] + xs, [\frac{s}{2}] + ys)
$$
1. Fully Convolutional One-Stage Object Detector
이 부분에서는 OB를 Pixel 단위로 예측하는 방식이 어떻게 진행되는지에 대해서 알아본다
- 기존의 Anchor Based Model은 기준점 $x, y$를 Box의 중심으로 가정하고 그 위치로 부터 Anchor Box를 생성하는 방식으로 물체를 Detection 한다. 하지만 FCOS에서는 $x, y$ 좌표의 픽셀말다 해당하는 Class와 GT Box의 Border를 추측한다.
FCOS 상세 계산 방법
- $x, y$ 좌표의 픽셀의 분류된 class가 GT Box 안에 속하면서 class값과 같을 경우 Positive Sample로 생각한다
- 해당되지 않을 경우에는 negative Sample 간주하고, Background(class = 0)로 계산된다
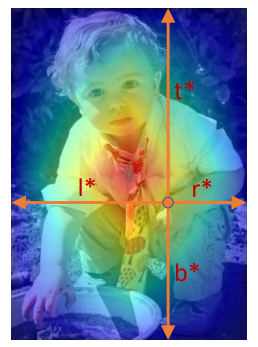
- $x, y$ 좌표의 class를 분류함과 동시에 4D vector $\mathbb{t}^* = (l^*, t^*, r^*, b^*)$ 에 대하여 Regresstion을 진행한다

- 여기서 $(l^*, t^*, r^*, b^*)$ 는 각각 $x, y$ 좌표에서부터 추측한 Bbox의 경계선 까지의 거리를 말하며 다음과 같이 나타낼 수 있다.
$$
l^* = x -x^{i}_{0} ,\quad t^* = y - y^{i}_{0}\\
r^* = x^{i}_{1} - x,\quad b^* = y^{i}_{1} - y
$$
- $x, y$에서 예측한 4차원 거리벡터와 GT box로 계산한 거리가 일치하도록 학습이 이루어진다
Network Output
- FCOS 에서는 Output으로 80-D의 Classfication Vector와 4-D의 Bbox vector $(l^*, t^*, r^*, b^*)$, Center-ness를 추정하도록 구성된다
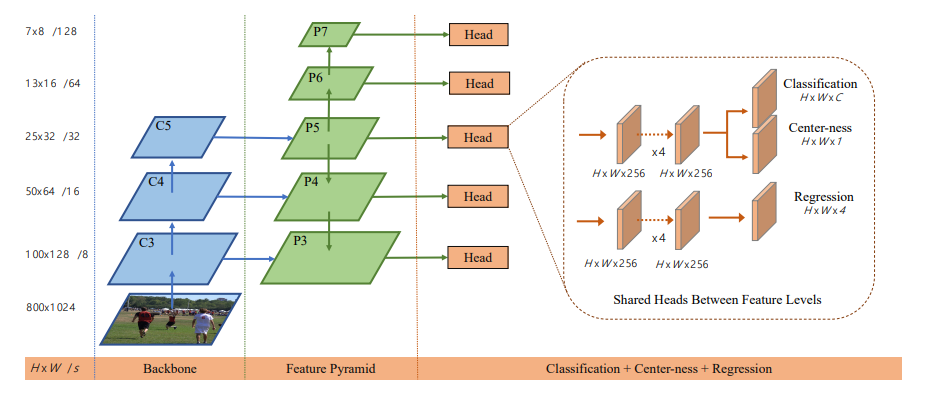
- 실제로는 Network에서 출력되는 값 $(l, t, r, b)$ 들을 exp를 통하여 변환시킨 값이 $(l^*, t^*, r^*, b^*)$가 된다
- 너무 큰 값을 출력으로 할 경우 학습에 문제가 생길 가능성이 존재하기 때문에 의도적으로 작은값을 출력하도록 설정하였다
- 80-D의 Classfication Vector는 multi-class classifier 구별되는 것이 아닌 각 class에 대해서 binary classification으로 예측된다
Loss
- Classification Loss는 Focal Loss를 사용
- Regression Loss는 IoUloss를 사용
- 그리고 각 Loss는 Positive sample 수만큼 나누어서 Normalization을 해주었다
Inference
- $p_{x, y}$ 가 threshold 이상일 경우에는 Positive Sample로 생각하여 Bbox를 Bbox vector를 통해서 예측하고 출력한다
2. Multi-level Prediction with FPN for FCOS
위의 항목에서 학습을 그대로 진행하면 Anchor Free Model의 고질적인 2가지의 문제점이 발생한다
- 작은 물체들은 stride가 큰 Feature map에서 표현이 되지 않기 때문에 Recall이 낮아진다
- GT Box가 겹쳐져 있을때 어느 GT에 맞춰서 Pixel이 학습을 해야하는지 모호함이 발생할 수 있다
이러한 문제점을 해결하기 위해서 논문에서는 FPN을 통한 Multi level Prediection을 제안하였다
Stride Problems
- FCOS에서는 FPN을 이용하여 다양한 stride를 누적을 통하여 표현
- 아래에 그림에서와 기본적인 FPN을 통해서 P3, P4, P5의 Layer를 생성한다
- P3, P4, P5는 각각 (8, 16, 32)의 누적된 stride를 가지고 있다
- P5에서 추가적으로 stride가 2로 설정된 CNN Layer를 2개 생성한다
- 생성된 P6, P7는 각각 64, 128의 누적된 stride를 가지고 있다
- FPN을 통해서 다양한 stride를 가지고 탐색을 진행한다
- 각 Level의 Layer에서 Box Regression을 진행할 때 $x, y$로 부터 예측되는 Bbox vector의 범위의 제한을 두고 제한을 넘어가면 Negative Sample로 취급한다
- 논문에서는 0, 64, 128, 256, 512, $\infty$ 로 설정하였다
ex) P3의 경우 0~64 제한
GT Box Overlap
- GT Box가 겹치는 경우 발생하는 모호함에 대해서 FPN구조로 어느정도 해결이 가능하다
- Overlap된 구간에 존재하는 Pixel들에 대해서 겹쳐지는 GT Box들간에 크기 차이가 존재할 경우 다른 Level의 Layer에서 예측될 가능성이 높다
- 그럼에도 불구하고 한 위치에 Layer 이상의 Box들이 할당이 되면은 면적이 가장 작은 GT Box를 사용한다
3. Center-ness
- 물체의 중앙점에서 먼 Pixel에서 예측된 Box Vector의 스코어가 낮은 경향을 보이는 문제가 존재하였다. 이것을 해결하기 위해 Center-ness를 도입하였다
- Box 외각의 pixel에서의 예측값은 classification을 통한 확률은 높아서 Positive sample로 판단 되었지만, 실제 Box Vector값은 잘 예측하지 못하는 경우가 많이 발생하였다
Center-ness
- 예측한 Box vector로 부터 $x, y$ 좌표가 Box의 Center에 가까울 수록 높은 가중치를 가지게 된다
$$
centerness = \sqrt{\frac{min(l^*, r^*)}{max(l^*, r^*)} \times \frac{min(t^*, b^*)}{max(t^*, b^*)}}
$$
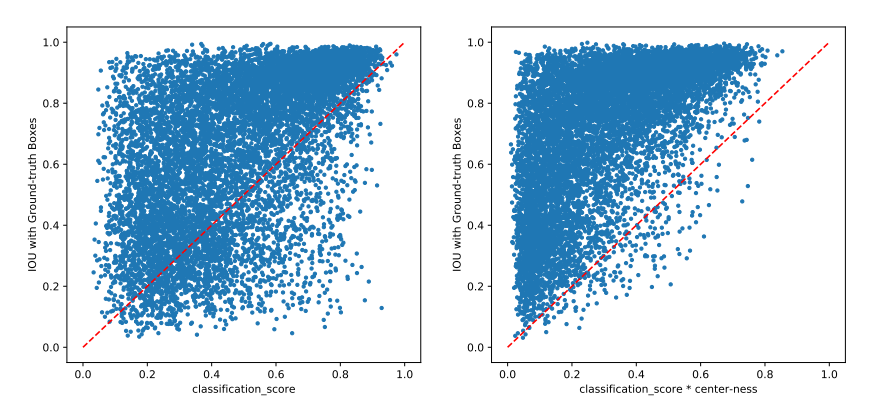
- classification score 출력에 center-ness를 곱해주면 마지막에 NMS를 진행할 때 낮은 score를 가지게 되기 때문에 걸러지게 만들 수 있다
- 논문에서는 center-ness를 도입해서 classfication score는 높지만 IoU score는 낮은 Sample들을 걸러내는 효과를 얻었다고 한다
결론
- Anchor Free 모델로 Anchor와 관련된 HyperParameter를 제외했다
- 다른 One stage Anchor Based Model과 비교해서 tuning이 없이도 비슷한 성능을 보여주었다
- Pixel Prediction(Semantic Segmentation) + Multi Label FPN + Center ness
- 전체 구조가 간단하면서도 좋은 성능을 보여주어서 응용성이 뛰어나다
- Two Stage Detecto의 RPN으로도 응용이 가능하다
후기
예전에 YoloX를 사용해 보면서 가볍게 보고 넘어갔던 논문이었는데 개념적으로만 일고 넘어가서 이번에 완전히 이해하는것을 목표로 리뷰를 해 보았다.
그동안 개념적으로 이런 논문이지를 알고 왜 그런것인지에 대해서 초점을 맞춰서 하나하나 읽고, 찾아가면서 공부를 했는데 퍼즐맞추는것처럼 나름 재미있었다! 그리고… 사실 다음주 P-Stage 대비용으로 하나두개 씩 읽어두는게 좋을거같아서 한것도 있다…ㅎ
마지막으로 영어공부를 하면서 해야겠다. 파파고가 너무 그동안 편했던것 같다