1. 오늘 하루 한 것

• 강의
  • CNN 4~6강, RNN 7강
• 정리
  • CNN 4~6강, RNN 7강
• 과제
  • CNN, RNN LSTM

2. 피어세션에서 한 것

• Batch norm weight 초기화에 관해서

3. 내일 할 것

• RNN 마무리, 논문리뷰 정리

4. 하루 느낀점

• 프로젝트 아이디어에 대해서 생각을 하는중이다 괜찮은게 있으려나?

Fully Convolutional Network

• CNN에서 마지막을 담당하던 Dense Layer를 Dense Layer Feature와 동일한 Channel수를 가진 Convolution Layer로 대체한 Network
• Dense Layer는 reshape을 통해서 input을 집어넣기 때문에 정해진 input size가 필요 했지만, convolution Layer의 경우 channel 이외에는 가변적이기 때문에 이미지의 크기와 상관없이 연산이 가능해졌다
• 연산을 할 때 마다 차원이 축소되는 문제가 있다 -> upsampling기법을 사용
  • conv transpose -> checker board
  • unpooling

Object Detection

R-CNN 계열

• R-CNN
  • Selective Search 로 BBox 2000개정도를 추출 한 뒤 각각 CNN을 돌린다
  • CNN 연산이 2000번 반복되기 때문에 매우 느린 속도이다
• fast R-CNN
  • SPP Net을 이용하여 기존 2000번 반복된 연산을 1번으로 줄임
• Faster R-CNN
  • Selective Search를 Region Proposal Network로 바꾼 R-CNN
  • Region Proposal Network : BBox도 네트워크 학습으로 뽑아내자
  • 기존에 존재하는 anchor Box(샘플한 여러 크기의 Bbox)와 이미지를 비교하여 물체가 있을법한 장소를 탐색하고, 대략적인 Bbox위치를 특정한다

Yolo

• BBox와 Classfication이 동시에 이루어지는 1 stage 모델
• R-CNN 계열에 비해서 속도가 매우 빠르지만, 정확도는 조금 떨어진다
• 실시간 물체검출이나 추적에 용이한 모델이다

reference

• Naver Connect Boostcamp - ai tech

AlexNet

• CNN으로 구성된 Network
• 시작부분에 11 x 11의 큰 convolution Layer를 사용했다

VGGNet

• 여러장의 3 x 3의 convolution Layer와 2 x 2 MaxPooling을 사용하였다
• 여러장의 3 x 3의 convolution Layer를 사용하면서 다음과 같은 advantage를 얻었다
  • 큰 convolution Layer와 동일한 연산을 더 작은 Parameter로 수행할 수 있다
  • receptive field를 크게 유지할 수 있다
  • 더 깊게 비선형적으로 Layer 추가가 가능해 진다

GoogLeNet

• 1 x 1, 3 x 3, 5 x 5, maxpooling을 이용하여 inception module을 구성하였다
• 1 x 1 convolution Layer를 이용해서 Channel 수를 줄여주었다

• Layer가 깊어지면서 Gradient Vanashing이 일어나는것을 막기위해 Auxiliary classifier를 두어서 추가적으로 Gradient를 더해주었다
  • inference시에는 사용되지 않는다

ResNet

• Skip Conncetion을 두어 Gradient Vanashing을 해결하여 더 많게 레이어를 쌓은 모델이다
• VGGnet의 3x3을 차용하여 파라미터 수를 크게 늘리지 않으면서 레이어를 더 쌓았다
• channel이 변하는 구간에서는 DownSampling을 통하여 channel과 Height, weight를 맞춰주었다

reference

• Naver Connect Boostcamp - ai tech

Convolution Neural Network (CNN)

• 시각적 데이터르 분석하는데 사용되는 인공신경망
• CNN은 크게 Convolution Layer, Pooling Layer, (Fully Cunnect Layer)로 구성된다

Convolution layer

• 합성곱 연산이 진행되는 레이어
• parameter의 수는 $kernel_size \times Channel_in \times Channel_out$으로 계산된다
• 이미지 처리를 할 시에 Fully Connected Layer보다 parameter 수가 월등하게 적다
• 실제 연산 이미지

• input과 output의 크기는 아래와 같이 계산된다
• input : $(N, C_{in}, H_{in}, W_{in})$
• output : $(N, C_{out}, H_{out}, W_{out})$
• stride : 연산이 이루어지는 간격
• padding : 차원을 확장시켜 convolution 연산후에도 크기가 일정하게 유지되도록 한다
• kernel : convolution 연산을 하는 주체, filter이기도 하다
• N : batch size
• C : Channel 수
• W : 연산될 Matrix의 가로 길이
• H : 연산될 Matrix의 세로 길이

Pooling Layer

• 일정 범위안의 값들을 대표하는 하나의 값으로 압축하는 down sampling 기법
• W와 H을 줄여서 차원을 축소하고, 연산에 필요한 parameter 수를 줄인다.

1x1 Convolution

• kernel size가 1,1인 convolution 연산을 하는것
• input, output의 W, H는 일정하지만 channel수가 감소한다.
• WHY?
  • channel 수를 줄여서 차원축소를 시키고, 추후에 연산에 필요한 parameter 수를 줄인다

$$
H_{out} = \left[ \frac{H_{in} + 2 \times \operatorname{padding[0]} - \operatorname{kernel_size[0]}}{\operatorname{stride}[0]} +1 \right]
$$

$$
W_{out} = \left[ \frac{W_{in} + 2 \times \operatorname{padding[1]} - \operatorname{kernel_size[1]}}{\operatorname{stride}[1]} +1 \right]
$$

reference

• Naver Connect Boostcamp - ai tech
• [By Aphex34 - Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=45679374]

1. 오늘 하루 한 것

• 강의
  • MLP, Optimization
• 정리
  • MLP, Optimization
• 과제
  • MLP, Optimization

2. 피어세션에서 한 것

• FQ
  • Regression Task, Classification Task, Probabilistic Task의 Loss 함수(or 클래스)는 Pytorch에서 어떻게 구현이 되어있을까요?
    *
  • 올바르게(?) cross-validation을 하기 위해서는 어떻 방법들이 존재할까요?
    • sklearn.model_selection.StratifiedKFold
  • Time series의 경우 일반적인 k-fold cv를 사용해도 될까요?
    • nested CV

3. 내일 할 것

• CNN, RNN 강의

4. 하루 느낀점

• 오늘은 열심히 한것같다

들어가기 전에

Generalization

• 이 모델이 얼마나 일반적인지를 나타내는 지표
• 보통 train loss와 test loss간의 차이를 말한다
• Generalization Gap이 작을수록 일반적인 모델이라고 한다

Overfitting & Underfitting

• Overfitting
  • 과적합. 학습데이터에 대해서는 잘 예측하지만, test데이터에 대해서는 잘 예측하지 못하는 형태.
• Underfitting
  • 학습데이터와 test데이터 둘 다 제대로 예측하지 못하는 형태.

Cross Vaildation

• Cross vaildation
  • train Data를 균등하게 나눠서 학습을 시켜 최적의 hyperparameter를 찾는 방법

Bias & Variance

• Bias
  • 편향
• Variance
  • 분산

Boostrapping 기법

• Bootstrapping
  • 통계학적으로 resampling을 통해 표본들의 추정치를 예측하는 기법
  • train dataset을 다시 sampling을 해서 만든 여러가지 data로 모델들을 학습시키는것을 Bootstrapping이라고 한다
• Bagging
  • Bootstrapping aggregating
  • 여러 모델들을 bootstrapping을 통하여 학습시키고, 그 나온 결과값의 평균을 내는 방법
  • 일반적으로 Ensemble 이라고 부른다
• Boosting
  • 여러개의 모델들을 학습시켜서 Sequential하게 이어 예측하는 방법

Gradient Descent Methods

• (Stochastic) gradient descent
  • 하나의 데이터 샘플로 Gradient를 업데이트 하는 방식
• Minibatch Gradient Descent
  • 일부의 데이터 샘플로 Gradient를 업데이트 하는 방식
• Batch Gradient Descent
  • 전체의 데이터로 Gradient를 업데이트 하는 방식
• 데이터의 전체 크기가 커진 현재로써 Batch Gradient는 하드웨어 한계와 연산속도가 Minibatch에 비해 느려서 현재는 대부분 Minibatch 형식으로 학습을 진행한다

Batch Size

• large batch -> sharp Minimum
• small batch -> Flat minimun

Optimization

1. (Stochastic) Gradient descent
   • 일반적인(확률적) 경사하강법
   • $\gamma$ : learning rate
   • $W$ : weight
   • $g$ : gradient
     $$
     W_{t+1} \leftarrow W_{t} - \gamma g_{t}
     $$
2. Momentum
   • 경사하강법에 관성을 부여한 방법
   • 전에 이동한 정보를 조금 더해서 Gradient를 업데이트 하는 방법
     $$
     \begin{aligned}
     a_{t+1} &\leftarrow \beta a_{t} + g_{t}\\
     W_{t+1} &\leftarrow W_{t} - \gamma a_{t+1}
     \end{aligned}
     $$
3. Nesterov Accelerate Gradient
   • Momentum과 비슷하지만 순서가 다르다
   • $a$ 방향으로 이동 한 뒤 위치에서 gradient를 계산 후 업데이트한다
   • Momentum 보다 minimum에 수렴하는 속도가 빠르다
     $$
     \begin{aligned}
     a_{t+1} &\leftarrow \beta a_{t} + \nabla\mathcal{L} (W_{t} - \gamma g_{t})\\
     W_{t+1} &\leftarrow W_{t} - \gamma a_{t+1}
     \end{aligned}
     $$
4. Adagrad
   • parameter의 변한 값에 대해서 영향을 받는다
   • $G_{t}$ : gradient 제곱합
   • 적게 변한 parameter는 크게, 크게변한 parameter는 작게 변환한다
   • $G_{t}$ 가 계속 커지기 때문에 학습이 길어지면 잘 학습되지 않는다
   • $G_{t}$ 또한 계속 저장해야하기 때문에 학습이 길어지면 resource 소모가 크다
     $$
     W_{t+1} \leftarrow W_{t} - \frac{\gamma}{\sqrt{G_{t}+\epsilon}} g_{t}
     $$
5. Adadelta
   • Adagrad에서 $G_{t}$ 가 무한하게 커지는것을 방지한 학습법
   • Weight에 관여하는 Learning rate가 존재하지 않는다
     • hyperparameter가 적어서 잘 사용되지 않았다
   • $G_{t}$ : EMA of gradient squares
   • $H_{t}$ : EMA of difference squares
   • EMA : Exponential Moving Average 지수이동평균
   • $\alpha$ : ema 가중치

$$
\begin{aligned}
G_{t+1} &\leftarrow \alpha G_{t} + (1-\alpha) g^{2}_{t}\\
W_{t+1} &\leftarrow W_{t} - \frac{\sqrt{H_{t-1}+\epsilon}}{\sqrt{G_{t}+\epsilon}} g_{t}\\
H_{t+1} &\leftarrow \alpha H_{t} + (1-\alpha)(\Delta W_{t})^2
\end{aligned}
$$

6. RMSprop
   • EMA of gradient squares + Learning rate
   • 해봤는데 잘되었다

$$
\begin{aligned}
G_{t+1} &\leftarrow \alpha G_{t} + (1-\alpha) g^{2}_{t}\\
W_{t+1} &\leftarrow W_{t} - \frac{\gamma}{\sqrt{G_{t}+\epsilon}} g_{t}
\end{aligned}
$$

7. Adam
   • RMSprop + Momentum
   • 현재 가장 많이 쓰이고있는 계열의 optimizer
   • AdamW, RAdam, AdamL등 여러가지 variation이 존재한다

$$
\begin{aligned}
m_{t+1} &\leftarrow \beta_{1} m_{t} + (1-\beta_{1}) g_{t}\\
v_{t+1} &\leftarrow \beta_{2} m_{t} + (1-\beta_{2}) v_{t}\\
W_{t+1} &\leftarrow W_{t} - \frac{\gamma}{\sqrt{v_{t}+\epsilon}}\frac{\sqrt{1-\beta^{t}_{2}}}{1-\beta_{1}^{t}} g_{t}
\end{aligned}
$$

Regularzation

• 일반화가 잘 되도록 데이터나 parameter에 규제를 하는 방법

1. Earlystopping
   • overfitting을 방지하기 위해서 중간에 학습을 멈추는것
   • 모델을 평가하기 위한 vaildation Dataset이 필요하다
2. Parameter norm penalty
   • 파라미터가 일정이상 커지는것을 방지하는 기법
3. Data augmentation
   • 데이터 수를 늘리기 위해 하는 기법
   • 데이터에 종류에 따라 augmentation을 잘 선택해서 반영해야한다
4. Noise robustness
   • 입력 데이터나, weight에 noise를 추가하는 기법
5. Label smoothing
   • 데이터의 경계를 흐리게 하여 강건성을 높이는 방법
   • Mix-up
     • 두 사진을 섞어서 섞은 비율만큼 다시 라벨링 하는 방법
   • Cutout
     • 일부분을 잘라서 제거하는 방법
   • CutMix
     • 일부분을 자른뒤 다른 label을 추가하는 방법
6. Dropout
   • 랜덤하게 일부 Neural을 비활성화 하는 방법
7. Batch normalization
   • 따로 포스팅 예정

reference

• Naver Connect Boostcamp - ai tech
• Bootstrapping Image
• Overfitting & Underfitting Image
• On Large-Batch Training for Deep Learning: Generalization Gap and Sharp Minima

Linear Neural Networks

• Data $(x_{i}, y_{i})^{N}_{i=1}$ 가 존재 할 때 $x$에 대해서 $\hat{y}$ 연산하는 선형연산함수
• $\hat{y}=Wx + b$
• $x$ : 데이터, $y$ : 라벨
• 경사하강법으로 y에 가까운 값을 계산하는 $W$와 $b$를 찾는다

Multi Layer Perceptron(MLP)

• 위의 Neural Network가 여러층에 걸쳐서 쌓여있는 형태
• Layer 사이에 Non Linear transform을 한다
  • 선형연산을 2번연속으로 하는것은 연산을 한번 하는 것과 똑같다
  • $W_{1}W_{2}x = W_{1,2}x$
• NonLinear transform의 역활을 해주는것이 Activation Functions이다
• 최근에는 대부분 ReLU 계열의 Activation Function이 쓰인다
• 자주 쓰이는 Activation functions
• Target $y$와 출력물 $\hat{y}$의 차이를 계산하는 loss function을 문제에 따라 잘 선택하여 사용하는 테크닉 또한 필요하다

그 외 내용

• 이론적으로 1개의 hidden layer로 대부분의 원하는 target값의 근사할 수 있다
  • 라고 하지만 이것은 매우 어렵다
  • 그만큼 Neural Network의 표현력이 좋다라는 뜻으로 받아드리는게 더 좋다.

reference

• Naver Connect Boostcamp - ai tech

Grid

• 축과 평행한 선을 사용하여 거리 및 값 등을 보조적으로 알려준다
• 색은 최대한 방해하지 않도록 무채색을 사용한다
• Layer상 항상 맨 아래 오도록 zorder를 0으로 조정
• axis를 이용해서 x, y축 또는 동시에 격자를 보이게 할 수 있다
• which 를 이용하여 큰격자, 세부격자 등을 보이게 할 수 있다

추가적인 보조 처리

• 보조선 긋기
  • axvline(), axhline()으로 수평선을 그을 수 있다
  • axvline(start, color, linestyle, zorder, alpha)

• start : 선을 그어질 point
• color : 색
• linestyle : 선 스타일
• zorder : z축 순서
• alpha : 투명도 조절

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

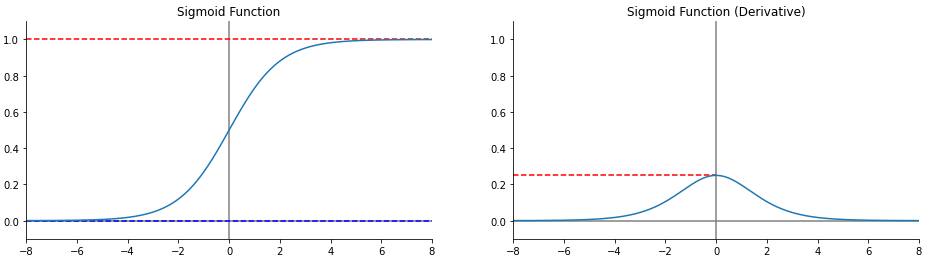
def drow_graph(x, y, d, function_name, y_lim, x_lim, minmax):
    fig, ax = plt.subplots(1, 2, figsize=(16, 4))

    ax[0].plot(x, y)
    ax[0].set_title(f"{function_name}")

    ax[1].plot(x, d)
    ax[1].set_title(f"{function_name} (Derivative)")
    if minmax:
        ax[0].axhline(max(y), color="red", linestyle="--", zorder=1)
        ax[0].axhline(min(y), color="blue", linestyle="--", zorder=1)
        ax[1].axhline(max(d), color="red", linestyle="--", zorder=1, xmax=0.5)

    for i in range(2):
        ax[i].axvline(0, color="gray", linestyle="-", zorder=0)
        ax[i].axhline(0, color="gray", linestyle="-", zorder=0)
        ax[i].set_xlim(x_lim)
        ax[i].set_ylim(y_lim)
        ax[i].spines['top'].set_visible(False)
        ax[i].spines['right'].set_visible(False)

• 보조 면 추가하기
  • axvspan(), axhspan()으로 영역에 색을 칠할 수 있다
  • axvspan(start, color, linestyle, zorder, alpha)

• start : 시작 point
• end : 끝 지점
• color : 색
• linestyle : 경계 스타일
• zorder : z축 순서
• alpha : 투명도 조절

1
2
3
4
5
6
7
8
9
10

fig, ax = plt.subplots()

ax.set_aspect(1)
ax.axvspan(0,0.5, color='red')
ax.axhspan(0,0.5, color='green')

ax.set_xlim(-1, 1)
ax.set_ylim(-1, 1)

plt.show()

reference

• Naver Connect Boostcamp - ai tech

Facet

• 분할을 의미한다
• 화면상에 view를 분할하여 큰틀에서는 볼 수 없는 부분집합을 세세하게 보여줄 수 있다.

1. Figure & Axes

• Figure는 그래프가 들어가는 큰 틀, Axes는 각 plot이 들어가는 공간을 말한다.
• Figure는 항상 1개, Axes는 여러개가 존재할 수 있다.
• 아래의 함수들로 N by M 의 Axes(subplot)들을 만들 수 있다.
  • plt.subplot()
  • plt.figure() + fig.add_subplot()
  • plt.subplots()
• sharex, sharey를 통해 subplot끼리의 x축, y축의 범위를 통일 할 수 있다
• squeeze를 False로 지정해서 subplot의 index를 n by m Matrix로 바꿀 수 있다.
  • 기본으로 True이기 때문에 1차원 배열로 나오게 된다
• aspect을 통해서 눈금간의 간격의 길이를 설정 할 수 있다

1
2
3
4

fig = plt.figure(figsize=(12, 5))
ax1 = fig.add_subplot(121, aspect=1)
ax2 = fig.add_subplot(122, aspect=0.5)
plt.show()

2. Grid spec

• css의 그리드 처럼 동일 크기 분할이 아닌 다양한 크기의 그래프를 그리고 싶을때 사용하는 방식이다
• add_subplot
  • numpy의 slicing과 비슷하게 사용이 가능하다

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

fig = plt.figure(figsize=(8, 5))
gs = fig.add_gridspec(3, 3)

ax = [None for _ in range(3)]

ax[0] = fig.add_subplot(gs[0, :2]) 
ax[0].set_title('gs[0, :]')

ax[1] = fig.add_subplot(gs[0:, -1])
ax[1].set_title('gs[0, -1]')

ax[2] = fig.add_subplot(gs[1:3, 0:2])
ax[2].set_title('gs[-1, 0]')

for ix in range(3):
    ax[ix].set_xticks([])
    ax[ix].set_yticks([])

plt.tight_layout()
plt.show()

• subplot2grid((shape), (y, x), colspan = dx, rowspan = dy)
  • shape를 통해 그리고자하는 grid를 설정
  • y, x : 시작하고자하는 좌표값
  • colspan, rawspan : 할당하고자 하는 가로 세로 길이

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

fig = plt.figure(figsize=(8, 5))
ax = [None for _ in range(6)]

ax[0] = plt.subplot2grid((3,4), (0,0), colspan=4)
ax[1] = plt.subplot2grid((3,4), (1,0), colspan=2)
ax[2] = plt.subplot2grid((3,4), (1,2), colspan=1)
ax[3] = plt.subplot2grid((3,4), (1,3), colspan=1,rowspan=2)
ax[4] = plt.subplot2grid((3,4), (2,0), colspan=3)

for ix in range(5): 
    ax[ix].set_title('ax[{}]'.format(ix)) # make ax title for distinguish:)
    ax[ix].set_xticks([]) # to remove x ticks
    ax[ix].set_yticks([]) # to remove y ticks
    
fig.tight_layout()
plt.show()

3. insert

• subplot 내부에 subplot을 생성하는 방법이다.
• ax.inset_axes()
  • Ax 내부에 subplot을 추가하는 방법
  • 메인 시각화를 해치지 않는 선에서 사용하자

1
2
3
4
5
6
7
8
9
10
11
12

fig, ax = plt.subplots()

color=['royalblue', 'tomato']
ax.bar(['A', 'B'], [1, 2],
       color=color
      )

ax.margins(0.2)
axin = ax.inset_axes([0.8, 0.8, 0.2, 0.2])
axin.pie([1, 2], colors=color, 
         autopct='%1.0f%%')
plt.show()

• make_axes_locatable(ax)
  • Ax 사이드에 부가적인 정보를 주는 방법
  • 보통 colorbar로 많이 사용한다

1
2
3
4
5
6
7
8
9
10
11

fig, ax = plt.subplots(1, 1)

# 이미지를 보여주는 시각화
# 2D 배열을 색으로 보여줌
im = ax.imshow(np.arange(100).reshape((10, 10)))

divider = make_axes_locatable(ax)
cax = divider.append_axes("right", size="5%", pad=0.05)

fig.colorbar(im, cax=cax)
plt.show()

reference

• Naver Connect Boostcamp - ai tech

color

• 시각화에서 색을 통해서 효과적으로 채널을 구분할 수 있다
• 심미적인 요소 또한 시각화의 일부 요소이다
• 전달하고 싶은 내용을 깔끔하게 색을 통해서 전달하는것이 주 목표이다
  • 꼭 화려한것이 답은 아니다

Color Palette

1. categorical color

• Discrete, Qualitative등의 다양한 이름으로 불린다
• 독립된 색상으로 구성되어 범주형 변수에 주로 사용된다
• 이산적인 개별값을 나타낼때 적합하다

2. Sequential color

• 정렬된 값을 가지는 연속형 변수에 적합나다
• 연속적인 색상을 사용하여 표현한다
  • 어두운곳에서는 밝은색, 밝은 곳에서는 어두운색을 이용한다.
• 색상은 단일 색조로 표현하는것이 좋다.
• 대표적으로 github commit log의 색이 있다.

3. Divergence color

• 연속형과 유사하지만 중앙을 기준으로 서로 다른색으로 나타난다
• 상반된 값을 표현하는데 좋다(기온, 지지율 등)

그 외에 고려할 점

• 다름을 보이기 위한 Highlighting을 색으로 표현 할 수 있다.
• 보통 먼 색일수록 차이가 더 크게보이는 색상 대비를 사용한다.
• 색약이나 색맹을 가지는 읽는 사람을 위해 색 선택을 고려할 필요가 있다.

reference

• Naver Connect Boostcamp - ai tech
• Sequential color