6. 베이즈 통계학

• 하나의 사건에서 믿음의 정도를 확률로 나타내는 베이즈 확률론에 기반한 통계학 이론
• 쉽게 말하면 아직 일어나지 않은 사건이 일어날 확률에 대한 계산을 하는 학문

6.0 조건부 확률

• 조건부확률 $P(A|B)$
  특정사건 $B$가 일어난 상황에서 사건 $A$가 일어날 확률이다. 아래와 같이 나타낼 수 있다.

  $A$와 $B$가 동시에 일어날 확률 = $B$가 일어날 확률 * $B$일어난 상황에서 $A$가 일어날 확률
  $$
  P(A\cap B) = P(B), P(A|B) = P(A), P(B|A)
  $$
  $$
  P(B|A) = \frac{P(A\cap B)}{P(A)} = P(B) \frac{P(A|B)}{P(A)}
  $$

6.1 베이즈 정리

• $D$ : 데이터

• $\theta$ : 측정하고싶은 파라미터

• 조건부 확률 $P(\theta|D)$는 사후확률이라고 부른다

• 조건부 확률 $P(D|\theta)$는 가능도(likehood, 우도)라고 부른다

• $P(\theta)$ 는 사전확률이라고 부른다

• 베이즈 정리는 아래와 같이 나타내며 이식으로 부터 우리는 사후확률과 가능도는 비례하는 관계임을 알 수 있다
  $$
  P(\theta|D) = P(\theta) \frac{P(D|\theta)}{P(D)}
  $$

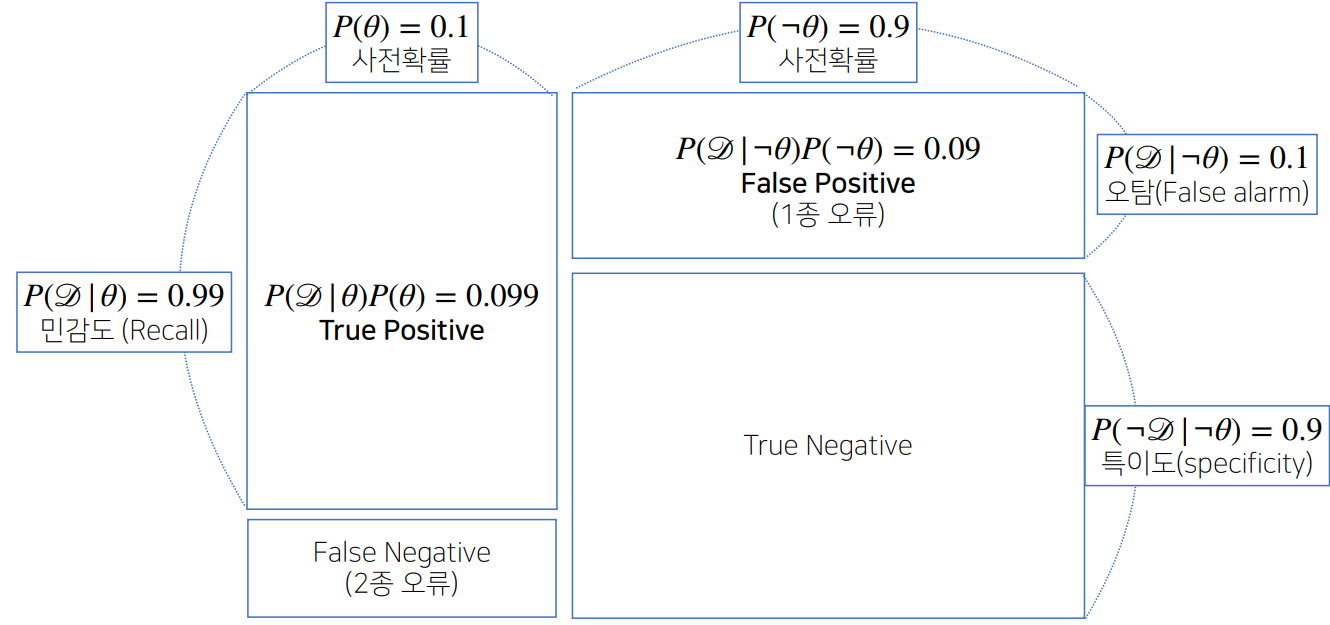
• 조건부 확률의 시각화

  • 정밀도(Precision) : 모델이 True라고 분류한 것들 중에서 실제 True인 것의 비율
  • 재현율(Recall) : 실제 True인 것 중에서 모델이 True라고 예측한 것의 비율
  • 정확도(Accuracy) : 올바르게 예측한 정도
    $$
    Precision = \frac{TP}{TP+FP}
    $$
    $$
    Recall = \frac{TP}{TP+FN}
    $$
    $$
    Accruacy = \frac{TP + TN}{TP+FN+FP+TN}
    $$

• 새로운 데이터가 들어왔을때 앞서 계산한 사후확률을 사전확률로 사용하여 새로운 사후확률로 갱신할 수 있다
  $$
  P^{\prime}(\theta|D) = P(\theta|D) \frac{P(D|\theta)}{P(D)}
  $$

• 조건부 확률은 일어나지 않은 일에 대해 유용한 통계적 해석을 제공하지만 인과관계를 추론할때는 함부로 사용해서는 안된다

• robust한 모델을 위해서는 인과관계를 생각할 필요가 있다

5. 통계학

• 다량의 데이터를 관찰하고 정리 분석하는 수학분야

5.0 용어정리

• 모집단 : 정보를 얻고자 하는 대상이 되는 집단의 전체
• 표본집단 : 모집단으로부터 추출한 데이터 집합
• 통계량 : 표본집단의 평균, 표준편차, 분산 등의 데이터를 말한다
• 표본분포 : 표본집단의 확률분포
• 표집분포 : 통계량의 확률분포

5.1 모수

• 모평균 모표준편차 모분산 등 모집단의 데이터를 말한다.
• 유한한 개수의 데이터를 관찰하는것으로 우리는 모집단의 분포를 정확하게 파악하는것은 불가능하기 때문에 근사적으로 확률분포를 추정해야한다
• 모수적 방법론
  • 데이터가 특정 확률분포를 따른다고 가정한 뒤 모수를 추정하는 방법
  • 보통 충분히 많은 데이터가 확보 되었을때 사용한다
• 비모수적 방법론
  • 확률분포를 가정하지 않고 데이터에 따라 모델의 구조 및 모수의 개수가 유연하게 바뀌는경우
  • 모수의 특성을 이용하지 않는다

5.2 확률분포를 가정하는 방법

• 데이터가 2개의 값 (0 또는 1)만 가지는 경우 $\rightarrow$ 베르누이 분포
• 데이터가 n개의 이산적인 값을 가지는 경우 $\rightarrow$ 카테고리 분포
• 데이터가 $[0,1]$ 사이에서 값을 가지는 경우 $\rightarrow$ 베타분포
• 데이터가 0 이상의 값을 가지는 경우 $\rightarrow$ 감마분포, 로그정규분포 등
• 데이터가 $\mathbb{R}$ 전체에서 값을 가지는 경우 $\rightarrow$ 정규분포, 라플라스분포 등

정규분포의 모수 평균과 분산

• 표본집단의 데이터를 $X$ 라고할때 표본평균 $\bar{X}$ 와 표본분산 $S^2$은 다음과 같다
  $$
  \bar{X} = \frac{1}{N}\sum_{i=1}^{N}X_{i}\qquad S^2 = \frac{1}{N-1}\sum_{i=1}^{N}(X_{i}-\bar{X})^2
  $$
• 이때 모집단의 모수인 평균 $\mu$ , 분산 $\sigma^2$ 표본평균과 표본분산의 기댓값으로 추정 할 수 있다
  $$
  {\displaystyle \operatorname {E}[\bar{X}]=\mu\quad\operatorname{E}[S^2] = \sigma^2}
  $$
• 통계량의 확률분포를 표집분포라고 부르며 표본평균의 표집분포는 $N$이 커질수록 정규분포를 따른다

5.3 최대 가능도 추정법 maximum likelihood estimation

• 이론적으로 가장 가능성이 높은 모수를 추정하는 방법 중 하나
• 어떤 상태 $\mathbf{x}$ 를 관측할 가능성이 제일 높은 모수를 추정하는 방법
  $$
  \hat{\theta}_{MLE} = \underset{\theta}{argmax}L(\theta; \mathbf{x}) = \underset{\theta}{argmax} P(\mathbf{x}|\theta)
  $$

5.4 KL divergence 쿨백-라이블러 발산

• 두 확률분포가 얼마나 떨어져 있는지를 나타낸다
• 거리로써 사용은 불가능하다
  • 역이 성립을 하지 않은다
• 솔직하게 여기에 정리하기에는 많이 중요한 내용이고 양도 많다
• 많이 중요하다 따로할 예정이다 그때 링크를 추가할 예정

4. 딥러닝 기본

• 딥러닝은 비선형모델인 신경망을 이용한 기계학습이다

4.1 softmax 함수

• 모델의 출력을 확률로 해석 할 수 있게 변환해주는 함수
• 인공신경망에서 확률분포를 얻기위한 마지막 활성함수로 많이 사용한다
• 출력값은 항상 0~1사이로 정규화된다
  $$
  f(x)_{k} = \frac{e^{x_i}}{\sum_{k=1}^{n}e^{x_{k}}}
  $$

4.2 Activation Function (활성함수)

• 실수범위에서 정의된 비선형 함수
• 딥러닝을 비선형 모델로 만들어주는 결정적인 함수이다
• 여러가지 종류가 있으며 ReLU계열이 제일 많이 사용되고 있다
• 포스팅을 통해 따로 다룰 예정이다

4.3 신경망

• 선형모델과 활성함수를 합성한 함수이다
• 우리가 흔히 부르는 MLP(Multi Layer Perceptron)는 여러 층의 합성신경망을 뜻한다

• $x$ : input
• $\sigma$ : Activation Function
• $h$ : Layer output
• $z$ : linear output
• $W$ : weight matrix
• $b$ : bias
  $$
  h = \sigma(z)\\
  z = Wx + b\\
  $$

4.4 Backpropagation

• MLP의 weight들을 효율적으로 갱신하는 알고리즘
• 합성함수의 미분법인 Chain-rule 기반으로 output Layer부터 input Layer로 미분을 계산해 나간다

$$
O = W_{2}h + b_{2}\\
h = \sigma(z)\\
z = W_{1}x + b_{1}\\
$$

5. 확률론

• 확률에 대해서 다루는 수학의 한 분야
• 딥러닝은 확률을 기반으로 한 머신러닝의 한 분야이기 때문에 그 기반에는 확률론이 깔려있다
  그래서 통계학을 배워야 한다
• 이 정리글에서 확률론에 대해 자세하게 다루지는 않을 예정이며 좀 더 자세한 글을 원한다면 PRML을 검색해서 보길 바란다

5.1 확률변수와 확률 분포

• 확률변수
  • 시행의 결과에 따라 값이 결정되는 변수를 나타낸다
  • 나타날 가능성이 있는 모든 경우의 수에 해당하는 값을 가질수 있다
  • ex) 주사위를 던질때 나올수 있는 눈
  • 확률분포에 따라서 이산확률변수와 연속확률변수 중 하나로 구분 될 수 있다
    • 항상 둘중 하나로 구분되는것은 아니다
• 확률분포
  • 확률변수가 특정한 값을 가질 확률을 나타내는 함수를 의미한다

5.2 이산확률와 연속확률

• 이산확률변수
  • 확률변수 X가 취할수 있는 모든값을 셀 수 있을때 이산확률변수라고 한다(가산변수)
  • 확률변수가 가질수 있는 모든 경우의 수를 고려하여 확률을 더해서 구한다
    $$
    \mathbb{P}(X\in A) = \sum_{x \in A}P(X=x)
    $$
• 연속확률변수
  • 연속적인 범위의 값을 지니는 확률변수. 모든 경우를 정확하게 셀 수 없는 확률변수이다(불가산변수)
  • 데이터 공간에 정의된 확률밀도함수의 적분을 통해 구한다
    $$
    \mathbb{P}(X\in A) = \int_{A}^{}P(\mathbf{x})d\mathbf{x}
    $$

5.3 결합확률 & 조건부확률

• 결합확률 $P(X, Y)$
  • $X=x$ 이고 $Y = y$ 일때의 확률을 나타내는 함수
• 조건부확률 $P(X | Y)$
  • $Y = y$ 일 때 $X = x$ 일 확률을 나타내는 함수
• 결합확률과 조건부확률은 다음과 같은 관계가 성립한다.
  $$
  P(x, y) = P(x|y)P(y) = P(y|x)P(x)
  $$
• 우리는 앞으로 이 조건부확률을 구하기 위해 모델을 학습시킨다

5.4 기댓값

• 각 사건이 벌어졌을때의 이득과 그 사건이 벌어질 확률의 곱을 전체 사건에대해 합한 값
• 이산확률일 경우

$$
\operatorname{E}[X]=\sum_{i}x_{i}P(x_{i})
$$

• 연속 확률일 경우

$$
\operatorname{E}[X]=\int_{X}xP(x)\operatorname {d} x
$$

• 또한 선형성을 가지고 있기 때문에 아래가 성립한다

$$
\operatorname{E}[X+Y]=\operatorname{E}[X]+\operatorname{E}[Y]
$$

$$
\operatorname{E}[cX]=c\operatorname{E}[X]
$$

• 조건부 기댓값
  • 조건부 확률에 대한 기댓값은 다음과 같이 계산한다

$$
\operatorname{E}[y|X]=\int_{Y}^{}yP(y|X)\operatorname{d}y
$$

5.5 몬테카를로 Sampling

• 반복된 무작위 추출을 이용하여 함수의 값을 근사하는 알고리즘
  • 표본공간의 확률분포에서 충분히 표본을 뽑으면 결국 확률분포에 근사한다
• 기계학습, 딥러닝을 학습시킬때 우리는 확률분포를 알지 못하는 경우가 대부분이기 때문에 데이터를 이요하여 기대값을 계산하려면 몬테카를로 방법을 이용해야한다
  $$
  {\displaystyle \operatorname {E} [f(x)] \approx \frac{1}{N} \sum_{i=1}^{N}f(x^{(i)}),\quad x(i) \overset{\underset{\mathrm{}}{i.i.d}}{\sim} P(x) }
  $$
• 독립추출만 보장되면 대수의법칙에 의해 항상 수렴성이 보장된다

이 글에서 미분은 다루지 않습니다

3. 경사하강법

• 함수의 극소값의 위치를 구할때 사용하는 방법
• 현재값의 기울기를 이용하여 점점 극소값에 접근한다
• 기울기가 너무 커서 발산할 경우를 방지하기 위해 lr(learning rate)를 곱해서 충분히 작은 값으로 계산을 해준다
• 컴퓨터로 계산할 경우 딱 떨어지는 정수를 만들어내기 힘들기 때문에 $\epsilon$ 값보다 작아질 경우를 수렴했다라고 가정한다

$$
x_{i+1} \leftarrow x_{i} - \gamma \nabla f(x_{i})
$$

• python code

  1 2 3 4 5

  var = init # 초기값 grad = gradient(var) # 현재 위치로부터 기울기를 구하는 함수 while (abs(grad) > eps): var += - lr * grad grad = gradient(var)

• 벡터가 입력인 다변수 함수의 경우는 편미분을 이용하여 경사하강법을 진행한다

3.1 선형회귀에서의 경사하강법

• 선형회귀에서의 target은 $\left\|\mathbf{y-X\beta}\right\|_{2}$ 이고, 이를 최소화하는 $\beta$를 찾아야 하기 때문에 아래와 같은 gradient를 구해야 한다

$$
\nabla_{\beta}\left\|\mathbf{y-X\beta}\right\|_{2}=-\frac{\mathbf{X^{\top}(y-X\beta)}}{n\left\|\mathbf{y-X\beta}\right\|_{2}}
$$

• 위의 식을 통하여 $\beta$를 구하는 경사하강법 알고리즘은 아래와 같다

$$
\begin{eqnarray*}
\beta_{i+1}&\leftarrow\beta_{i}-\gamma\nabla_{\beta}\left\|\mathbf{y-X\beta_{i}}\right\|_{2}\\
\beta_{i+1}&\leftarrow\beta_{i} + \gamma \frac{\mathbf{X^{\top}(y-X\beta)}}{n\left\|\mathbf{y-X\beta}\right\|_{2}}
\end{eqnarray*}
$$

• 간략하게 아래와 같이 표현도 가능하다
  • gradient를 최소화시키는것과 gradient의 제곱을 최소화 시키는것은 같은 의미

$$
\beta_{i+1} \leftarrow \beta_{i} + \frac{2\gamma}{n} \mathbf{X^{\top}(y-X\beta)}
$$

3.2 경사하강법의 한계

• 볼록한 함수에서는 적절한 학습률과 반복횟수를 선택했을 때 수렴이 보장되어있다
• 비선형회귀의 경우 목적식이 볼록하지 않기 때문에 수렴이 항상 보장되지는 않는다
• 특히 딥러닝의 경우 고차원의 자료를 다루기 때문에 경사하강법만으로는 학습하기가 힘들다

• 이러한 이유로 SGD, Momentom, Adam 등의 여러가지 optimize 알고리즘이 등장했다
• 이 부분에 대해서는 추후에 따로 다룰 예정이다

14. Exception Handing

• 사전에 인지했거나 예측 하지못한 각종의 예외들을 대처하기위한 방법
• 개발자가 반드시 명시적으로 정의해야한다
• try ~ except

1
2
3
4

try:
    예외 발생 가능 코드
except (exception 종류):
    예외 발생시 대응하는 코드

• try ~ except ~ else
  • else : 예외가 발생하지 않을때 진행하는 부분

1
2
3
4
5
6

try:
    예외 발생 가능 코드
except (exception 종류):
    예외 발생시 대응하는 코드
else:
    예외가 발생하지 않을 때 동작하는 코드

• try ~ except ~ finally
  • finally : 예외가 발생해도 진행하는 부분

1
2
3
4
5
6

try:
    예외 발생 가능 코드
except (exception 종류):
    예외 발생시 대응하는 코드
finally:
    예외에 상관없이 동작하는 코드

• 기본적으로 제공하는 exception 종류 : 링크
• raise 함수를 사용하여 강제로 Error나 Exception을 발생시킬 수 있다.

15. File Handing

• 코드로 파일을 처리하기 위한 방법
• 파일 처리를 위해서 open 을 사용한다

  1 2 3 4

  f = open('파일이름', '접근모드') ... ... f.close()

  모드	설명
  r	읽기모드 - 파일 내용을 읽어올 때 사용
  w	쓰기모드 - 파일 내용을 수정할 때 사용
  a	추가모드 - 파일에 내용을 추가할 때 사용
  b	바이너리 모드 - 바이너리형식으로 파일을 읽기/수정/추가할 때 사용
  +	파일을 읽고 쓰기용으로 열기 (앞의 모드에 따라서 파일 포인터의 위치차이가 존재한다)
  x	쓰기모드로 생성하는데 이미 파일이 존재할 경우 예외를 발생시킨다

16. Logging Handling

• Log
  프로그램이 실행되는 동안 일어 나는 정보를 말한다. 이런 기록들을 모아 분석하여 의미있는 결과를 도출 할 수 있기 때문에 Log를 따로 관리하는 모듈을 사용한다
• Python의 기본 Log 관리모듈 logging이 존재한다
• logging level에 관련한 표 : 아래로 내려갈수록 높은 레벨의 log이다

12. Module 모듈

• 작은 프로그램 조각
  이 조각들을 모아서 하나의 큰 프로그램을 만든다
• 사용하는 이유 : 다른 프로그램에서 사용하기가 편하다
  편하면 무조건 해야지
• module == .py 파일
• import 문을 사용하여 같은폴더 내의 module 이나 package를 호출한다
• module을 호출하는 방법
  1. 별칭으로 호출
  2. 특정 함수 또는 클래스만 호출
  3. 모듈에 모든 함수또는 클래스를 호출

1
2
3

import numpy as np  # 1
from numpy import ndarray  # 2
from numpy import *  # 3

• python에는 수많은 Built-in Modules이 존재한다
  • random, tqdm, time, collection, heap, Math …

13. package

• 다양한 모듈이 모여서 이루어진 코드 묶음
• 오픈소스들이 모두 패키지로 관리된다
• 각 폴더별로 필요한 모듈을 구현하고, __init__.py를 구성한다
• 추후에 __init__.py 와 __main__.py 작성법에 관련되어 포스팅을 할 예정이다

11. Object Oriented Programming (객체 지향적 프로그래밍, OOP)

• 객체(Object)란?
  프로그램에서 사용되는 데이터 또는 식별자에 의해 참조되는 공간, 독립된 단위를 의미한다
• OOP는 여러개의 독립된 객체들의 모임으로 프로그램을 구성하는것을 이야기한다

11.1 Object in Python

• Python에서의 객체는 class로 선언이 가능하다

• class는 속성(Attribute)와 명령어(Method)을 가지고 있다

  • Attribute
    해당 class가 가지고 있는 특별한 변수를 말한다. 이 변수는 다른 객체가 될 수도 있다. __init__(self) 메서드로 속성을 미리 설계할 수 있다
  • Method
    해당 class가 내장하고 있는 함수들을 지칭한다. 메서드는 class 안에 기존 함수와 같은 방식으로 정의가 가능하나, 반드시 self를 추가해야 메서드로 인정된다. 또한 python에는 특별한 메서드 들이 존재한다

• class의 이름 선언과 함께 __init__메서드에 parameter 값들을 입력하면 객체를 생성 할 수 있다

• class_name.method_name()과 같은 형식으로 객체의 메서드를 호출 할 수 있다

• 예시 축구선수

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

class SoccerPlayer(object):
    def __init__(self, name, position, back_number):
        self.name = name
        self.position = position
        self.back_number = back_number
        
    def change_back_number(self, new_number):
        print("선수의 등번호를 변경합니다 : From %d to %d" % (self.back_number, new_number))
        self.back_number = new_number
        
    def kick(self):
        pass
    
    def heading(self):
        pass
    
    def moving(self):
        pass

jinhyun = SoccerPlayer("Jinhyun", "MF", 10)
print("현재 선수의 등번호는 :", jinhyun.back_number)
jinhyun.change_back_number(5)
print("현재 선수의 등번호는 :", jinhyun.back_number)
==================================================
output:
현재 선수의 등번호는 : 10
선수의 등번호를 변경합니다 : From 10 to 5
현재 선수의 등번호는 : 5

11.1.1 Special method

• class에는 __init__ 과 같이 특정한 일을 전담하는 정해진 메서드들이 존재하고 이것들을 Special method라고 부른다
• class 내부에 Special method를 정의하면 객체간의 operator 연산 등 여러가지를 할 수 있다.
• 자세한 내용은 링크로 남기고 생략한다.
• 여러가지 스페셜 메서드

11.2 OOP의 특징

• Visibility 가시성
  • 객체의 정보를 볼수 있는 레벨을 조절한다
  • 유저에게 필요한 부분은 보여주고(추상화), 노출할 필요가 없는 정보들은 숨긴다(캡슐화)
  • __ 를 속성이나 메서드 앞에 붙여서 객체 외부에서 접근할 수 없게 한다
  • 결론 : docstring 잘 쓰는게 중요하다
• Inheritance 상속
  • 부모클래스로부터 속성과 Method를 물려받은 자식클래스를 생성 하는 것을 말한다
  • super를 통해 부모클래스의 메서드를 호출 할 수 있다
  • 코드의 재사용이 목적이다
• polymorphism 다형성
  • 같은 이름의 메서드의 내부로직을 다르게 사용할 수 있다.
  • 자식클래스에서 메서드를 재정의(overiding)하여 새로 맞춰서 사용이 가능하다

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

class TeamAPlayer(SoccerPlayer):
    def __init__(self, regular):
        super().__init__(name, position, back_number)
        self.regular = regular
    
    def is_regular(self):
        print(self.name, '선수는 주전', '입니다' if self.regular else '이 아닙니다')
    
    def change_back_number(self, new_number):
        print(f"팀 A {self.name}선수의 등번호를 변경합니다")
        super().change_back_number()
        self.back_number = new_number

jinhyun = TeamAPlayer("Jinhyun", "MF", 10, False)
jinhyun.is_regular()
jinhyun.change_back_number(5)
=============================
output:
Jinhyun 선수는 주전 이 아닙니다
팀 A Jinhyun선수의 등번호를 변경합니다
선수의 등번호를 변경합니다 : From 10 to 5

참고 자료

객체 지향 프로그래밍 - wikipedia

10. Pythonic Code

• Python 스타일의 효율적인 코딩기법
• 사용하면 코드를 간결하고 이쁘게 작성할 수 있다. 그리고 잘하는 사람처럼 보인다
  • 그러니 모두 잘 익히고 사용하자

10.1 List comprehension

• 기존의 list를 사용하여 간단한 list를 만드는 기법
• for 문 + list.append 보다 속도가 빠르다
• 조건문과 함께 더 다양한 list를 표현 가능하다

  1 2 3 4 5 6

  # 기존 방법 a = [] for i in range(10): a.append(i) # list comprehension a = [i for i in range(10)]

10.2 enumerate & zip

• enumerate
  • for 문에서 iterable object의 element를 추출할 때 인덱스 번호와 함께 추출

    1 2 3 4 5

    for i, x in enumerate('apple'): print(i, x) # 0 a, 1 p, ... , 4 e list(enumerate('apple')) output = [(0, 'a'), (1, 'p'), (2, 'p'), (3, 'l'), (4, 'e')]

• zip
  • 여러개의 list값을 병렬적으로 추출해서 하나의 list로 재결합 시킨다.

    1 2 3 4 5

    a = (1, 2, 3) b = (4, 5, 6) print(list(zip(a, b))) ###################### [(1, 4), (2, 5), (3, 6)]

10.3 map & lambda & reduce

• map
  • iterable object의 element에 각각 특정한 함수를 적용할 수 있는 함수
  • 아래의 lambda와 병행하여 자주, 많이 쓰인다
  • 실행시점의 값을 생성해서 메모리를 효율적으로 사용한다

    1 2 3 4 5 6 7

    def function(x): return x**2 a = [1, 2, 3, 4, 5] print(list(map(function, a))) ############################# output => [1, 4, 9, 16, 25]

• lambda
  • 함수를 따로 정의할 필요 없이 사용할 수 있는 익명 함수
  • PEP8에서 권장하지는 않지만 아직도 많이쓰고 스스로도 많이 쓰고있다
    • 어려운 문법, 테스트하기 힘듬, docstring 지원안함, 코드해석이 어려움 등등의 문제가 있다
  • 간단한 명령문인 경우 따로 정의하지 않고 lambda를 사용하는 편이다

    1 2 3 4

    a = [1, 2, 3, 4, 5] print(list(map(lambda x: x**2, a))) ############################# output => [1, 4, 9, 16, 25]

• reduce
  • map과 비슷한 동작으로 list에 똑같은 함수를 적용해서 합쳐나간다
  • 2년 넘게 공부하면서 한번도 쓴적이 없다
  • python3 버전에서 lambda와 같이 사용을 권장하지 않는다

    1 2	from functools import reduce print(reduce(lambda x, y: x+y, [1, 2, 3, 4, 5]))

10.4 iterable object

• 시퀸스형 자료형에서 데이터를 순서대로 추출하는 object
• object 내부적으로 __iter__와 __next__라는 함수(메서드)가 존재한다
• .iter() 와 .next() 함수로 iterable 객체를 iterator object로 사용이 가능하다
• 아래의 generator와 같이 사용하면 정말 강력한 성능을 보이게 된다

  1 2 3 4 5 6 7 8 9 10 11 12

  cities = ["Seoul", "Busan", "Jeju"] iter_obj = iter(cities) print(next(iter_obj)) print(next(iter_obj)) print(next(iter_obj)) next(iter_obj) ============== output: Seoul Busan Jeju Error 발생 더이상 출력할 수 있는 원소가 없음

10.5 generator

• iterable object를 특수한 형태로 사용해주는 함수

• object 내부의 element가 호출되는 시점에 값을 메모리에 반환한다

  • yield를 사용해서 한번에 하나의 element만 반환함
    • 이 것이 궁금하다면 python 코루틴 관련해서 찾아보는것이 좋다

• 일반적인 iterator 보다 generator가 훨씬더 적은 메모리를 사용한다

• 먼 훗날에 나올 Dataset이 generator를 이용한 object이다

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27

  def my_gen(): n = 1 print('This is printed first') # Generator function contains yield statements yield n n += 1 print('This is printed second') yield n n += 1 print('This is printed at last') yield n # Using for loop for item in my_gen(): print(item) ===================== output: This is printed first 1 This is printed second 2 This is printed at last 3

  예제출처

• generator도 list comprehension과 유사한 형태로 표현이 가능하다

• [] 대신 ()로 표현한다.

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

  gen_ex = (n*n for n in range(500)) print(next(gen_ex)) # 0 1 4 .... ``` ### 10.6 function passing arguments * 함수에 입력되는 Argument는 아래와 같이 다양한 형태를 가진다 * Keyword arguments * 함수에 입력되는 parameter의 변수명을 같이 입력하여 순서에 상관없이 parameter를 지정 해 줄 수 있다 ```python def function(a, b): return a*2 + b print(function(3, 5)) print(function(b=5, a=3)) ========================= output: 11 11

  • Default arguments

    • parameter의 기본값을 사용한다
    • 따로 argument가 입력되지 않을 경우 기본값으로 출력한다

      1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28

      def function(a, b=0): return a*2 + b print(function(3, 1)) print(function(3)) ================== output: 7 6 ``` * Variable-length arguments(가변인자) * 개수가 특정되지 않은 변수를 함수의 parameter로 사용하는 방법 * Asterist * 기호를 사용하여 argument를 나타낸다 * 입력된 값은 Tuple로 사용할 수 있다 * 함수에서 단 하나 존재하고, 뒤에 일반적인 argument가 존재할 수 없다 ```python def asterisk_test(a, b, *args): print(args) return a+b+sum(args) print(asterisk_test(1, 2, 3, 4, 5)) =================================== output: (3, 4, 5) 튜플의 형태로 존재한다 15

  • Keyword Variable-length arguments(키워드 가변인자)

    • Parameter의 이름을 따로 지정하지않고 입력하는 방법
    • Asterisk 두개 (**) 를 사용하여 함수의 parameter를 표시한다
    • 입력된 값은 dict type으로 사용할수 있다
    • 함수에서 단 하나 존재하고 뒤에 다른 argument가 존재할 수 없다

1
2
3
4
5
6
7
8

def asterisk_test(a, b, **kargs):
    print(kargs)
    return a+b+sum(kargs.values())
print(asterisk_test(1, 2, three=3, four=4, five=5))
===================================================
output:
{'three': 3, 'four': 4, 'five': 5}
15

10.7 Asterisk

• Asterisk는 위의 가변인자와 곱하기 연산자 이외의 기능이 존재한다
• list, tuple 등의 자료형 변수 앞에 *를 붙여서 unpacking 할 수 있다
• dict type의 경우 **를 붙여서 키워드 가변인자처럼 출력이 가능하다

  1 2 3 4 5 6 7 8 9 10 11 12 13

  a = [1, 2, 3, 4] print(a) print(*a) b = {'one':1, 'two':2, 'three':3} print(*b) print(asterisk_test(1, 2, **b)) =============================== output: [1, 2, 3, 4] 1 2 3 4 one two three {'one': 1, 'two': 2, 'three': 3} 9

9. 데이터 구조

• Stack & Queue
• Tuple & Set
• Dictionary
• Collection

9.1 Stack & Queue

• Stack
  • 나중에 넣은 데이터를 먼저 반환하도록 설계된 데이터 구조
  • LIFO (Last in First Out)
  • 입력을 Push, 출력을 Pop이라고 한다
  • python의 list는 기본적으로 Stack의 구조를 가진다
• Queue
  • 먼저 넣은 데이터가 먼저 반환하도록 설계된 데이터 구조
  • FIFO (First in First Out)
  • 입력은 Push, 출력은 get 이라고 한다
  • 보통 python의 Dequeue를 사용한다.
• 정해진 크기를 넘어갈 경우 overflow, element가 없는데 반환을 시킬경우 underflow라고 한다.

9.2 Tuple & Set

• Tuple
  • 값의 변경이 불가능한 리스트
  • index로 접근해서 값을 수정하는것을 막는다
  • 정의 할 때 ( )를 사용한다
  • 리스트와 동일하게 (+, *)연산, Indexing, Slicing을 사용한다
  • 사용자의 실수에 의한 에러를 사전에 방지하기 위해 변경할 필요가 없는 데이터를 저장할 때 사용한다

1
2
3

t = (1, ) # 값이 1개인 Tuple은 반드시 ,를 붙여야 함
t + t # (1, 1)
t[0] = 2 # Error 발생함

• Set
  • 값을 순서없이 저장, 중복을 허용하지 않는 자료형(확인필요)
  • set( )을 통하여 객체를 생성한다
  • set을 이용하여 다양한 집합연산이 가능하다

    1 2 3 4 5 6 7 8

    s1 = set([1, 2, 3, 4, 5]) s2 = set([1, 3, 5, 7, 9]) s1.union(s2) # (1, 2, 3, 4, 5, 7, 9) 합집합 s1 | s2 # (1, 2, 3, 4, 5, 7, 9) 합집합 s1.intersection(s2) # (1, 3, 5) 교집합 s1 & s2 # (1, 3, 5) 교집합 s1.difference(s2) # (2, 4) 차집합 s1 - s2 # (2, 4) 차집합

9.3 Dictionary

• 데이터를 저장 할 때 구분지을수 있는 값(Key)를 함께 저장
• Hash 구조
• Key값을 활용하여 Value를 관리한다.
• dict( )나 { }로 객체를 생성한다

1
2
3
4
5
6
7
8
9
10

number_dic = {'one': 1, 'two': 2, 'three': 3}
number_dic['one'] # 1, Key 값으로 value 출력 가능
country_code.items() # 데이터 출력
# dict_items([('one', 1), ('two', 2), ('three', 3)])
number_dic.keys() # key만 출력
# dict_keys(['one', 'two', 'three'])
number_dic.values() # value만 출력
# dict_values([1, 2, 3])
number_dic.get(1) # None, 아닐경우 None
number_dic.get('one') # 1, key가 존재할 경우 values 값을 return

9.4 Collections

• Python Built-in 확장 모듈

• 편의성, 실행 효율 등을 사용자에게 제공함

• 자주 사용되는 deque, difaultdict, Counter에 대해서만 다룰것이다

• deque

  • Stack과 Queue의 기능을 모두 지원하는 데이터 구조
  • List에 비해 효율적인 저장방식을 지원한다
    • popleft()등 삽입 삭제에 매우 효율적임
  • Linked List의 특성(rotate, reverse)을 지원한다
  • 기존 list 형태의 함수를 모두 지원함

    1 2 3 4 5

    from collections import deque q = deque() q.append(a) # [a] q.appendleft(b) # [b, a] q.popleft() # [a]

• defaultdict

  • Dict type값에 기본값을 지정해서 key가 존재하지 않아도 기본값으로 찾아지는 기능을 가지고 있다
  • defaultdict(datatype) 으로 기본값의 자료형을 정하면서 dict객체를 생성할 수 있다

    1 2 3 4

    from collections import defaultdict dic = defaultdict(int) dic['a'] += 1 # {'a': 1} dic['b'] -= 1 # {'a': 1, 'b': -1}

• Counter

  • 시퀸스 type의 data element들의 갯수를 dict형태로 변환

    1 2 3

    from collections import Counter c = Counter([1, 3, 5, 3, 2, 4, 3]) # Counter({1: 1, 3: 3, 5: 1, 2: 1, 4: 1})