---

8. RNN

• 연속적인 데이터(Sequence Data)를 주로 다루는 Nerual Network
• 소리, 문자열, 주가등의 데이터를 분석하는데 사용된다

8.1 시계열 데이터

• 독립동등분포 가정을 잘 위배하기 때문에 순서를 바꾸거나 과거에 정보에 손실이 발생하면 데이터의 확률분포 자체가 변해버린다

• 베이즈 법칙을 이용하여 다음과 같이 표현이 가능하다
  $$
  \begin{aligned}
  P(X_1, … ,X_{t}) & = P(X_t|X_1, …, X{t-1})P(X_1,…,X_{t-1})\\
  & = \prod_{s=1}^{t}P(X_s|X_{s-1},…,X_1)
  \end{aligned}
  $$

• 시퀸스 데이터를 다루기 위해서는 길이가 가변적인 데이터를 다룰수 있는 모델이 필요하다

  • 조건부에 들어가는 데이터의 길이는 시퀸스마다 가변적이다
    $$
    \begin{aligned}
    X_t &\sim P(X_t|X_{t-1}, … X_{1})\\
    X_{t+1} &\sim P(X_t|X_{t}, X_{t-1}, … X_{1})
    \end{aligned}
    $$

• 고정된길이 $\tau$ 만큼의 시퀸스만 사용하는 모델의 경우 자기회귀모델(Autoregressive Model)이라고 한다

  • 매우 오래된 과거의 데이터는 실제 데이터에 큰 영향을 주기 힘들다는 가정하에 세워진 모델이다
    $$
    \begin{aligned}
    X_t &\sim P(X_t|X_{t-1}, … X_{t-\tau})\\
    X_{t+1} &\sim P(X_t|X_{t}, … X_{t-\tau+1})
    \end{aligned}
    $$

• 이전정보를 제외한 나머지 정보들을 잠재변수로 활용하는 모델을 잠재자기회귀모델 이라고 한다

  • 앞으로 다룰 RNN도 이 모델에 해당한다
    $$
    \begin{aligned}
    X_t &\sim P(X_t|X_{t-1}, H_t)\\
    X_{t+1}&\sim P(X_t|X_{t}, H_{t+1})\\
    H_t&=\operatorname{Net}(H_{t-1}, X_{t-1})
    \end{aligned}
    $$

8.2 RNN

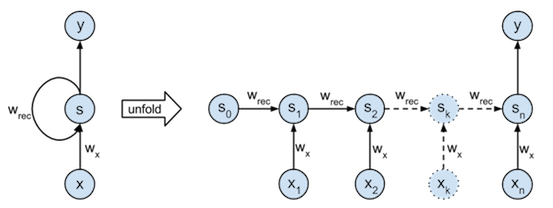
• 기본적인 RNN 모델은 아래와 같이 MLP와 유사한 형태를 가지고 있다
• RNN은 이전순서의 잠재변수와 현재의 입렬을 활용하여 계산을 이어나간다
• RNN의 역전파는 BPTT(Backpropagation Through Time)라고 불리며 연결그래프에 따라 순차적으로 계산한다

  • $S$ : 잠재변수
  • $X$ : input Data
  • $W_x$ : $X$의 가중치행렬
  • $W_{rec}$ : $S$의 가중치 행렬
  • $\sigma$ : Activate Function
  • $X$ : 시퀸스 데이터

• RNN의 Network 연산

$$
\mathbf{S_{t}} = \sigma (\mathbf{O}_{t-1} + \mathbf{X}_{t}\mathbf{W}_{x})
$$
$$
\mathbf{O_{t}} = \mathbf{S}_{t}\mathbf{W}_{rec}
$$

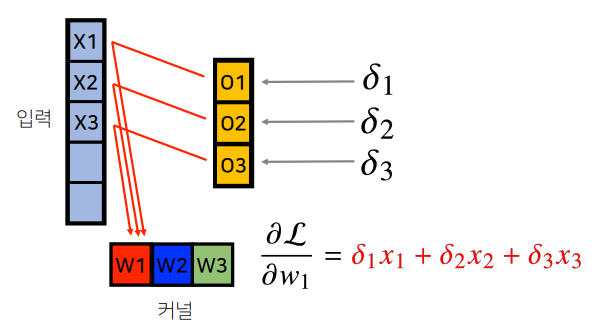
• BPTT
  • RNN의 Backpropagation 을 계산해보면 미분의 곱으로 이루어진 항이 계산된다
  • 시퀸스의 길이만큼의 $W_{rec}$의 역전파가 이루어 질 때 마다 계속해서 미분을 하기 때문에 시퀸스의 길이가 길어질수록 gradient vanishing(기울기 소실)이 발생하여 계산이 불안정해 진다

    • $L$ : loss 함수
    • $y$ : target

$$
\frac{\partial S_{t}}{\partial W_{rec}} = \sum_{i=1}^{t-1} \left( \prod_{j=i+1}^{t} \frac{\partial S_{j}}{\partial S_{j-1}} \right)\frac{\partial S_{i}}{\partial W_{rec}} + \frac{\partial S_{t-1}}{\partial W_{rec}}
$$

• truncated BPTT
  • RNN은 시퀸스의 길이가 길어지면 기울기 소실이 발생하여 계산이 불안정해지기 때문에 중간에 연산을 끊어주는 테크닉.
• 이러한 기울기 소실을 해결하기 위해 등장한 네트워크
  • LSTM, GRU

---

7. CNN

• 합성곱을 이용한 신경망

7.1 Convolution 연산

• 신호(signal)를 커널을 이용해서 국소적으로 증폭 또는 감소시키는 연산을 말한다

• CNN 에서 하는 연산은 엄밀하게 말하면 Cross Correlation 연산이다

  • Cross Correlation
    $$
    [f*g](x) = \int_{\mathbb{R}}f(z)g(x+z)\operatorname{d}z
    $$
  • Convolution 연산
    $$
    [f*g](x) = \int_{\mathbb{R}}f(z)g(x-z)\operatorname{d}z
    $$

• 다양한 차원에서 연산이 가능하다
  $$
  \begin{aligned}
  &1D \quad [f*g](i) = \sum_{p=1}^{d}f(p)g(i+p)\\
  &2D \quad [f*g](i,j) = \sum_{p,q}f(p,q)g(i+p,j+q)\\
  &3D \quad [f*g](i,j,k) = \sum_{p,q,r}f(p)g(i+p,j+q,k+r)
  \end{aligned}
  $$

7.1 2D Convolution 연산

• 2차원 convolution 연산은 커널을 input위에서 움직여가면서 선형모델과 합성함수가 적용되는 구조이다.

• 출력크기는 아래와 같이 계산된다

  • $H, W$ : 입력크기
  • $K_{h}, K_{w}$ : 커널의 크기
  • $O_{h}, O_{w}$ : 출력의 크기
    $$
    O_{h} = H-K_{h}+1\\
    O_{w} = W-K_{w}+1
    $$

7.2 Convolution 연산의 Backpropagation

• Convolution 연산의 역전파도 결국에는 선형연산이 여러번 적용된 형태이기 때문에 계산할때 각 커널의 들어오는 모든 gradient를 더하면 된다

$$
\frac{\partial \mathcal{L}}{\partial w_{i}} = \sum_{j} \delta_{j} x_{i+j-1}
$$

---

6. 베이즈 통계학

• 하나의 사건에서 믿음의 정도를 확률로 나타내는 베이즈 확률론에 기반한 통계학 이론
• 쉽게 말하면 아직 일어나지 않은 사건이 일어날 확률에 대한 계산을 하는 학문

6.0 조건부 확률

• 조건부확률 $P(A|B)$
  특정사건 $B$가 일어난 상황에서 사건 $A$가 일어날 확률이다. 아래와 같이 나타낼 수 있다.

  $A$와 $B$가 동시에 일어날 확률 = $B$가 일어날 확률 * $B$일어난 상황에서 $A$가 일어날 확률
  $$
  P(A\cap B) = P(B), P(A|B) = P(A), P(B|A)
  $$
  $$
  P(B|A) = \frac{P(A\cap B)}{P(A)} = P(B) \frac{P(A|B)}{P(A)}
  $$

6.1 베이즈 정리

• $D$ : 데이터

• $\theta$ : 측정하고싶은 파라미터

• 조건부 확률 $P(\theta|D)$는 사후확률이라고 부른다

• 조건부 확률 $P(D|\theta)$는 가능도(likehood, 우도)라고 부른다

• $P(\theta)$ 는 사전확률이라고 부른다

• 베이즈 정리는 아래와 같이 나타내며 이식으로 부터 우리는 사후확률과 가능도는 비례하는 관계임을 알 수 있다
  $$
  P(\theta|D) = P(\theta) \frac{P(D|\theta)}{P(D)}
  $$

• 조건부 확률의 시각화

  • 정밀도(Precision) : 모델이 True라고 분류한 것들 중에서 실제 True인 것의 비율
  • 재현율(Recall) : 실제 True인 것 중에서 모델이 True라고 예측한 것의 비율
  • 정확도(Accuracy) : 올바르게 예측한 정도
    $$
    Precision = \frac{TP}{TP+FP}
    $$
    $$
    Recall = \frac{TP}{TP+FN}
    $$
    $$
    Accruacy = \frac{TP + TN}{TP+FN+FP+TN}
    $$

• 새로운 데이터가 들어왔을때 앞서 계산한 사후확률을 사전확률로 사용하여 새로운 사후확률로 갱신할 수 있다
  $$
  P^{\prime}(\theta|D) = P(\theta|D) \frac{P(D|\theta)}{P(D)}
  $$

• 조건부 확률은 일어나지 않은 일에 대해 유용한 통계적 해석을 제공하지만 인과관계를 추론할때는 함부로 사용해서는 안된다

• robust한 모델을 위해서는 인과관계를 생각할 필요가 있다

---

5. 통계학

• 다량의 데이터를 관찰하고 정리 분석하는 수학분야

5.0 용어정리

• 모집단 : 정보를 얻고자 하는 대상이 되는 집단의 전체
• 표본집단 : 모집단으로부터 추출한 데이터 집합
• 통계량 : 표본집단의 평균, 표준편차, 분산 등의 데이터를 말한다
• 표본분포 : 표본집단의 확률분포
• 표집분포 : 통계량의 확률분포

5.1 모수

• 모평균 모표준편차 모분산 등 모집단의 데이터를 말한다.
• 유한한 개수의 데이터를 관찰하는것으로 우리는 모집단의 분포를 정확하게 파악하는것은 불가능하기 때문에 근사적으로 확률분포를 추정해야한다
• 모수적 방법론
  • 데이터가 특정 확률분포를 따른다고 가정한 뒤 모수를 추정하는 방법
  • 보통 충분히 많은 데이터가 확보 되었을때 사용한다
• 비모수적 방법론
  • 확률분포를 가정하지 않고 데이터에 따라 모델의 구조 및 모수의 개수가 유연하게 바뀌는경우
  • 모수의 특성을 이용하지 않는다

5.2 확률분포를 가정하는 방법

• 데이터가 2개의 값 (0 또는 1)만 가지는 경우 $\rightarrow$ 베르누이 분포
• 데이터가 n개의 이산적인 값을 가지는 경우 $\rightarrow$ 카테고리 분포
• 데이터가 $[0,1]$ 사이에서 값을 가지는 경우 $\rightarrow$ 베타분포
• 데이터가 0 이상의 값을 가지는 경우 $\rightarrow$ 감마분포, 로그정규분포 등
• 데이터가 $\mathbb{R}$ 전체에서 값을 가지는 경우 $\rightarrow$ 정규분포, 라플라스분포 등

정규분포의 모수 평균과 분산

• 표본집단의 데이터를 $X$ 라고할때 표본평균 $\bar{X}$ 와 표본분산 $S^2$은 다음과 같다
  $$
  \bar{X} = \frac{1}{N}\sum_{i=1}^{N}X_{i}\qquad S^2 = \frac{1}{N-1}\sum_{i=1}^{N}(X_{i}-\bar{X})^2
  $$
• 이때 모집단의 모수인 평균 $\mu$ , 분산 $\sigma^2$ 표본평균과 표본분산의 기댓값으로 추정 할 수 있다
  $$
  {\displaystyle \operatorname {E}[\bar{X}]=\mu\quad\operatorname{E}[S^2] = \sigma^2}
  $$
• 통계량의 확률분포를 표집분포라고 부르며 표본평균의 표집분포는 $N$이 커질수록 정규분포를 따른다

5.3 최대 가능도 추정법 maximum likelihood estimation

• 이론적으로 가장 가능성이 높은 모수를 추정하는 방법 중 하나
• 어떤 상태 $\mathbf{x}$ 를 관측할 가능성이 제일 높은 모수를 추정하는 방법
  $$
  \hat{\theta}_{MLE} = \underset{\theta}{argmax}L(\theta; \mathbf{x}) = \underset{\theta}{argmax} P(\mathbf{x}|\theta)
  $$

5.4 KL divergence 쿨백-라이블러 발산

• 두 확률분포가 얼마나 떨어져 있는지를 나타낸다
• 거리로써 사용은 불가능하다
  • 역이 성립을 하지 않은다
• 솔직하게 여기에 정리하기에는 많이 중요한 내용이고 양도 많다
• 많이 중요하다 따로할 예정이다 그때 링크를 추가할 예정

---

4. 딥러닝 기본

• 딥러닝은 비선형모델인 신경망을 이용한 기계학습이다

4.1 softmax 함수

• 모델의 출력을 확률로 해석 할 수 있게 변환해주는 함수
• 인공신경망에서 확률분포를 얻기위한 마지막 활성함수로 많이 사용한다
• 출력값은 항상 0~1사이로 정규화된다
  $$
  f(x)_{k} = \frac{e^{x_i}}{\sum_{k=1}^{n}e^{x_{k}}}
  $$

4.2 Activation Function (활성함수)

• 실수범위에서 정의된 비선형 함수
• 딥러닝을 비선형 모델로 만들어주는 결정적인 함수이다
• 여러가지 종류가 있으며 ReLU계열이 제일 많이 사용되고 있다
• 포스팅을 통해 따로 다룰 예정이다

4.3 신경망

• 선형모델과 활성함수를 합성한 함수이다
• 우리가 흔히 부르는 MLP(Multi Layer Perceptron)는 여러 층의 합성신경망을 뜻한다

• $x$ : input
• $\sigma$ : Activation Function
• $h$ : Layer output
• $z$ : linear output
• $W$ : weight matrix
• $b$ : bias
  $$
  h = \sigma(z)\\
  z = Wx + b\\
  $$

4.4 Backpropagation

• MLP의 weight들을 효율적으로 갱신하는 알고리즘
• 합성함수의 미분법인 Chain-rule 기반으로 output Layer부터 input Layer로 미분을 계산해 나간다

$$
O = W_{2}h + b_{2}\\
h = \sigma(z)\\
z = W_{1}x + b_{1}\\
$$

---

5. 확률론

• 확률에 대해서 다루는 수학의 한 분야
• 딥러닝은 확률을 기반으로 한 머신러닝의 한 분야이기 때문에 그 기반에는 확률론이 깔려있다
  그래서 통계학을 배워야 한다
• 이 정리글에서 확률론에 대해 자세하게 다루지는 않을 예정이며 좀 더 자세한 글을 원한다면 PRML을 검색해서 보길 바란다

5.1 확률변수와 확률 분포

• 확률변수
  • 시행의 결과에 따라 값이 결정되는 변수를 나타낸다
  • 나타날 가능성이 있는 모든 경우의 수에 해당하는 값을 가질수 있다
  • ex) 주사위를 던질때 나올수 있는 눈
  • 확률분포에 따라서 이산확률변수와 연속확률변수 중 하나로 구분 될 수 있다
    • 항상 둘중 하나로 구분되는것은 아니다
• 확률분포
  • 확률변수가 특정한 값을 가질 확률을 나타내는 함수를 의미한다

5.2 이산확률와 연속확률

• 이산확률변수
  • 확률변수 X가 취할수 있는 모든값을 셀 수 있을때 이산확률변수라고 한다(가산변수)
  • 확률변수가 가질수 있는 모든 경우의 수를 고려하여 확률을 더해서 구한다
    $$
    \mathbb{P}(X\in A) = \sum_{x \in A}P(X=x)
    $$
• 연속확률변수
  • 연속적인 범위의 값을 지니는 확률변수. 모든 경우를 정확하게 셀 수 없는 확률변수이다(불가산변수)
  • 데이터 공간에 정의된 확률밀도함수의 적분을 통해 구한다
    $$
    \mathbb{P}(X\in A) = \int_{A}^{}P(\mathbf{x})d\mathbf{x}
    $$

5.3 결합확률 & 조건부확률

• 결합확률 $P(X, Y)$
  • $X=x$ 이고 $Y = y$ 일때의 확률을 나타내는 함수
• 조건부확률 $P(X | Y)$
  • $Y = y$ 일 때 $X = x$ 일 확률을 나타내는 함수
• 결합확률과 조건부확률은 다음과 같은 관계가 성립한다.
  $$
  P(x, y) = P(x|y)P(y) = P(y|x)P(x)
  $$
• 우리는 앞으로 이 조건부확률을 구하기 위해 모델을 학습시킨다

5.4 기댓값

• 각 사건이 벌어졌을때의 이득과 그 사건이 벌어질 확률의 곱을 전체 사건에대해 합한 값
• 이산확률일 경우

$$
\operatorname{E}[X]=\sum_{i}x_{i}P(x_{i})
$$

• 연속 확률일 경우

$$
\operatorname{E}[X]=\int_{X}xP(x)\operatorname {d} x
$$

• 또한 선형성을 가지고 있기 때문에 아래가 성립한다

$$
\operatorname{E}[X+Y]=\operatorname{E}[X]+\operatorname{E}[Y]
$$

$$
\operatorname{E}[cX]=c\operatorname{E}[X]
$$

• 조건부 기댓값
  • 조건부 확률에 대한 기댓값은 다음과 같이 계산한다

$$
\operatorname{E}[y|X]=\int_{Y}^{}yP(y|X)\operatorname{d}y
$$

5.5 몬테카를로 Sampling

• 반복된 무작위 추출을 이용하여 함수의 값을 근사하는 알고리즘
  • 표본공간의 확률분포에서 충분히 표본을 뽑으면 결국 확률분포에 근사한다
• 기계학습, 딥러닝을 학습시킬때 우리는 확률분포를 알지 못하는 경우가 대부분이기 때문에 데이터를 이요하여 기대값을 계산하려면 몬테카를로 방법을 이용해야한다
  $$
  {\displaystyle \operatorname {E} [f(x)] \approx \frac{1}{N} \sum_{i=1}^{N}f(x^{(i)}),\quad x(i) \overset{\underset{\mathrm{}}{i.i.d}}{\sim} P(x) }
  $$
• 독립추출만 보장되면 대수의법칙에 의해 항상 수렴성이 보장된다

---

이 글에서 미분은 다루지 않습니다

3. 경사하강법

• 함수의 극소값의 위치를 구할때 사용하는 방법
• 현재값의 기울기를 이용하여 점점 극소값에 접근한다
• 기울기가 너무 커서 발산할 경우를 방지하기 위해 lr(learning rate)를 곱해서 충분히 작은 값으로 계산을 해준다
• 컴퓨터로 계산할 경우 딱 떨어지는 정수를 만들어내기 힘들기 때문에 $\epsilon$ 값보다 작아질 경우를 수렴했다라고 가정한다

$$
x_{i+1} \leftarrow x_{i} - \gamma \nabla f(x_{i})
$$

• python code

  1 2 3 4 5

  var = init # 초기값 grad = gradient(var) # 현재 위치로부터 기울기를 구하는 함수 while (abs(grad) > eps): var += - lr * grad grad = gradient(var)

• 벡터가 입력인 다변수 함수의 경우는 편미분을 이용하여 경사하강법을 진행한다

3.1 선형회귀에서의 경사하강법

• 선형회귀에서의 target은 $\left\|\mathbf{y-X\beta}\right\|_{2}$ 이고, 이를 최소화하는 $\beta$를 찾아야 하기 때문에 아래와 같은 gradient를 구해야 한다

$$
\nabla_{\beta}\left\|\mathbf{y-X\beta}\right\|_{2}=-\frac{\mathbf{X^{\top}(y-X\beta)}}{n\left\|\mathbf{y-X\beta}\right\|_{2}}
$$

• 위의 식을 통하여 $\beta$를 구하는 경사하강법 알고리즘은 아래와 같다

$$
\begin{eqnarray*}
\beta_{i+1}&\leftarrow\beta_{i}-\gamma\nabla_{\beta}\left\|\mathbf{y-X\beta_{i}}\right\|_{2}\\
\beta_{i+1}&\leftarrow\beta_{i} + \gamma \frac{\mathbf{X^{\top}(y-X\beta)}}{n\left\|\mathbf{y-X\beta}\right\|_{2}}
\end{eqnarray*}
$$

• 간략하게 아래와 같이 표현도 가능하다
  • gradient를 최소화시키는것과 gradient의 제곱을 최소화 시키는것은 같은 의미

$$
\beta_{i+1} \leftarrow \beta_{i} + \frac{2\gamma}{n} \mathbf{X^{\top}(y-X\beta)}
$$

3.2 경사하강법의 한계

• 볼록한 함수에서는 적절한 학습률과 반복횟수를 선택했을 때 수렴이 보장되어있다
• 비선형회귀의 경우 목적식이 볼록하지 않기 때문에 수렴이 항상 보장되지는 않는다
• 특히 딥러닝의 경우 고차원의 자료를 다루기 때문에 경사하강법만으로는 학습하기가 힘들다

• 이러한 이유로 SGD, Momentom, Adam 등의 여러가지 optimize 알고리즘이 등장했다
• 이 부분에 대해서는 추후에 따로 다룰 예정이다