들어가기 전에
Generalization
- 이 모델이 얼마나 일반적인지를 나타내는 지표
- 보통 train loss와 test loss간의 차이를 말한다
- Generalization Gap이 작을수록 일반적인 모델이라고 한다
Overfitting & Underfitting
- Overfitting
- 과적합. 학습데이터에 대해서는 잘 예측하지만, test데이터에 대해서는 잘 예측하지 못하는 형태.
- Underfitting
- 학습데이터와 test데이터 둘 다 제대로 예측하지 못하는 형태.
Cross Vaildation
- Cross vaildation
- train Data를 균등하게 나눠서 학습을 시켜 최적의 hyperparameter를 찾는 방법
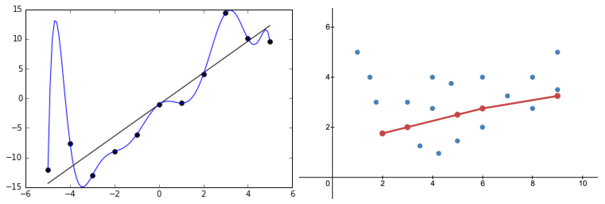
Bias & Variance
Boostrapping 기법
- Bootstrapping
- 통계학적으로 resampling을 통해 표본들의 추정치를 예측하는 기법
- train dataset을 다시 sampling을 해서 만든 여러가지 data로 모델들을 학습시키는것을 Bootstrapping이라고 한다
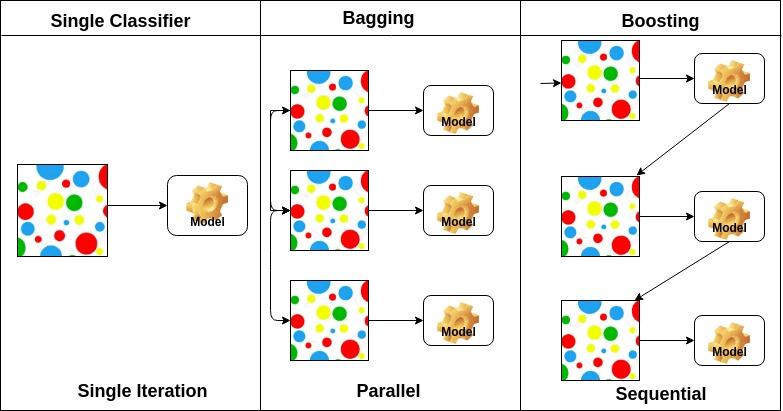
- Bagging
- Bootstrapping aggregating
- 여러 모델들을 bootstrapping을 통하여 학습시키고, 그 나온 결과값의 평균을 내는 방법
- 일반적으로 Ensemble 이라고 부른다
- Boosting
- 여러개의 모델들을 학습시켜서 Sequential하게 이어 예측하는 방법
Gradient Descent Methods
- (Stochastic) gradient descent
- 하나의 데이터 샘플로 Gradient를 업데이트 하는 방식
- Minibatch Gradient Descent
- 일부의 데이터 샘플로 Gradient를 업데이트 하는 방식
- Batch Gradient Descent
- 전체의 데이터로 Gradient를 업데이트 하는 방식
- 데이터의 전체 크기가 커진 현재로써 Batch Gradient는 하드웨어 한계와 연산속도가 Minibatch에 비해 느려서 현재는 대부분 Minibatch 형식으로 학습을 진행한다
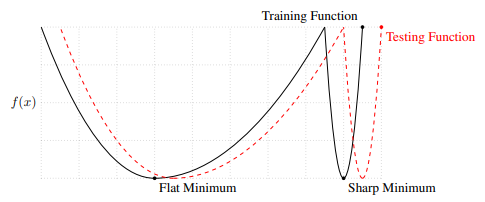
Batch Size
- large batch -> sharp Minimum
- small batch -> Flat minimun
Optimization
- (Stochastic) Gradient descent
- 일반적인(확률적) 경사하강법
- $\gamma$ : learning rate
- $W$ : weight
- $g$ : gradient
$$
W_{t+1} \leftarrow W_{t} - \gamma g_{t}
$$
- Momentum
- 경사하강법에 관성을 부여한 방법
- 전에 이동한 정보를 조금 더해서 Gradient를 업데이트 하는 방법
$$
\begin{aligned}
a_{t+1} &\leftarrow \beta a_{t} + g_{t}\\
W_{t+1} &\leftarrow W_{t} - \gamma a_{t+1}
\end{aligned}
$$
- Nesterov Accelerate Gradient
- Momentum과 비슷하지만 순서가 다르다
- $a$ 방향으로 이동 한 뒤 위치에서 gradient를 계산 후 업데이트한다
- Momentum 보다 minimum에 수렴하는 속도가 빠르다
$$
\begin{aligned}
a_{t+1} &\leftarrow \beta a_{t} + \nabla\mathcal{L} (W_{t} - \gamma g_{t})\\
W_{t+1} &\leftarrow W_{t} - \gamma a_{t+1}
\end{aligned}
$$
- Adagrad
- parameter의 변한 값에 대해서 영향을 받는다
- $G_{t}$ : gradient 제곱합
- 적게 변한 parameter는 크게, 크게변한 parameter는 작게 변환한다
- $G_{t}$ 가 계속 커지기 때문에 학습이 길어지면 잘 학습되지 않는다
- $G_{t}$ 또한 계속 저장해야하기 때문에 학습이 길어지면 resource 소모가 크다
$$
W_{t+1} \leftarrow W_{t} - \frac{\gamma}{\sqrt{G_{t}+\epsilon}} g_{t}
$$
- Adadelta
- Adagrad에서 $G_{t}$ 가 무한하게 커지는것을 방지한 학습법
- Weight에 관여하는 Learning rate가 존재하지 않는다
- hyperparameter가 적어서 잘 사용되지 않았다
- $G_{t}$ : EMA of gradient squares
- $H_{t}$ : EMA of difference squares
- EMA : Exponential Moving Average 지수이동평균
- $\alpha$ : ema 가중치
$$
\begin{aligned}
G_{t+1} &\leftarrow \alpha G_{t} + (1-\alpha) g^{2}_{t}\\
W_{t+1} &\leftarrow W_{t} - \frac{\sqrt{H_{t-1}+\epsilon}}{\sqrt{G_{t}+\epsilon}} g_{t}\\
H_{t+1} &\leftarrow \alpha H_{t} + (1-\alpha)(\Delta W_{t})^2
\end{aligned}
$$
- RMSprop
- EMA of gradient squares + Learning rate
- 해봤는데 잘되었다
$$
\begin{aligned}
G_{t+1} &\leftarrow \alpha G_{t} + (1-\alpha) g^{2}_{t}\\
W_{t+1} &\leftarrow W_{t} - \frac{\gamma}{\sqrt{G_{t}+\epsilon}} g_{t}
\end{aligned}
$$
- Adam
- RMSprop + Momentum
- 현재 가장 많이 쓰이고있는 계열의 optimizer
- AdamW, RAdam, AdamL등 여러가지 variation이 존재한다
$$
\begin{aligned}
m_{t+1} &\leftarrow \beta_{1} m_{t} + (1-\beta_{1}) g_{t}\\
v_{t+1} &\leftarrow \beta_{2} m_{t} + (1-\beta_{2}) v_{t}\\
W_{t+1} &\leftarrow W_{t} - \frac{\gamma}{\sqrt{v_{t}+\epsilon}}\frac{\sqrt{1-\beta^{t}_{2}}}{1-\beta_{1}^{t}} g_{t}
\end{aligned}
$$
Regularzation
- 일반화가 잘 되도록 데이터나 parameter에 규제를 하는 방법
- Earlystopping
- overfitting을 방지하기 위해서 중간에 학습을 멈추는것
- 모델을 평가하기 위한 vaildation Dataset이 필요하다
- Parameter norm penalty
- Data augmentation
- 데이터 수를 늘리기 위해 하는 기법
- 데이터에 종류에 따라 augmentation을 잘 선택해서 반영해야한다
- Noise robustness
- 입력 데이터나, weight에 noise를 추가하는 기법
- Label smoothing
- 데이터의 경계를 흐리게 하여 강건성을 높이는 방법
- Mix-up
- 두 사진을 섞어서 섞은 비율만큼 다시 라벨링 하는 방법
- Cutout
- CutMix
- 일부분을 자른뒤 다른 label을 추가하는 방법
- Dropout
- 랜덤하게 일부 Neural을 비활성화 하는 방법
- Batch normalization
reference