부스트 캠프 ai tech 8주 2일차 Sementic Segmantation
Semantic segmentation
- 이미지의 픽셀단위로 Classification을 수행하는 Task
- 의료분야에서나 자율주행, 영상편집 등의 분야에서 다양하게 사용된다.
Fully Convolutional Networks (FCN)
- KeyPoint : 기존 fully connected Layer(fc Layer)를 Convolutional Layer로 대체하면서 fc Layer의 문제점을 해결하고 Semantic Segmentation까지 end to end로 구현한 모델
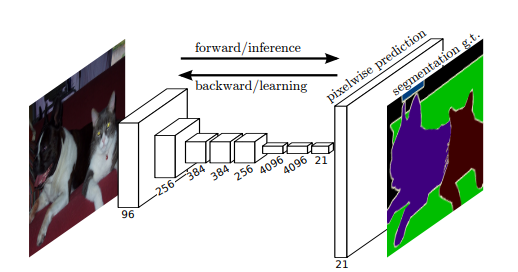
기존의 Classification 모델들은 마지막 Layer를 fc Layer로 구성하기 때문에 고정된 input 이미지 사이즈를 가져야 했지만 1 x 1 Convolution Layer를 사용하면서 가변적인 input 이미지를 사용할 수 있게 되었다
맨 마지막 단에 Upsampling을 시행하여 해상도를 맞춰주어 Segmentation을 한다
- Transposed Convolution
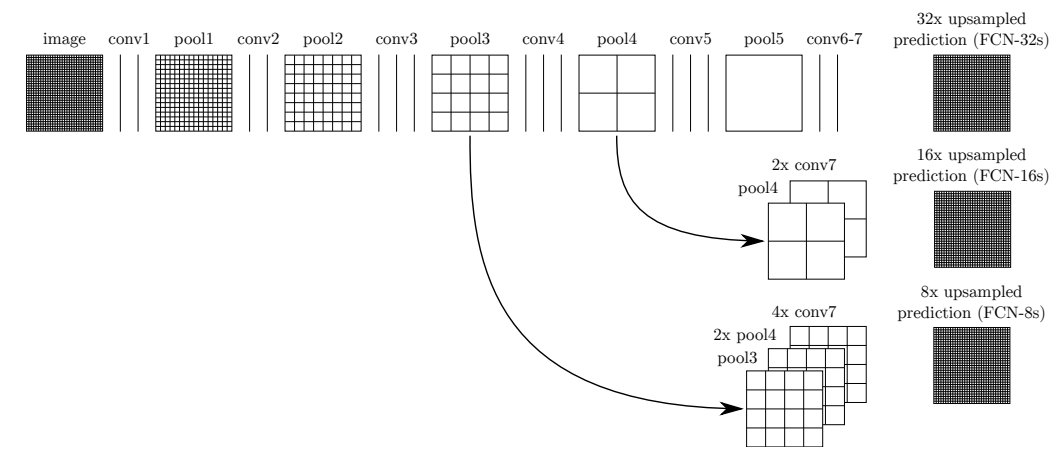
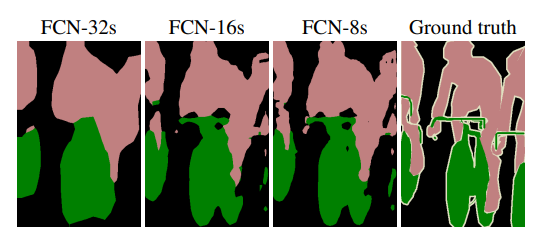
아래와 같은 특징을 골고루 가지기 위해 중간단계의 map을 Upsampling을 해서 가져와 더한다. 단계별 Map들이 합쳐지면서 더 좋은 Segmantaion 이 가능했다.
- Layer를 적게 거칠수록 이미지의 지역적이고 세부적인 부분에 집중한다
- Layer를 많이 지나가면 이미지의 전체적인 부분에 집중한다
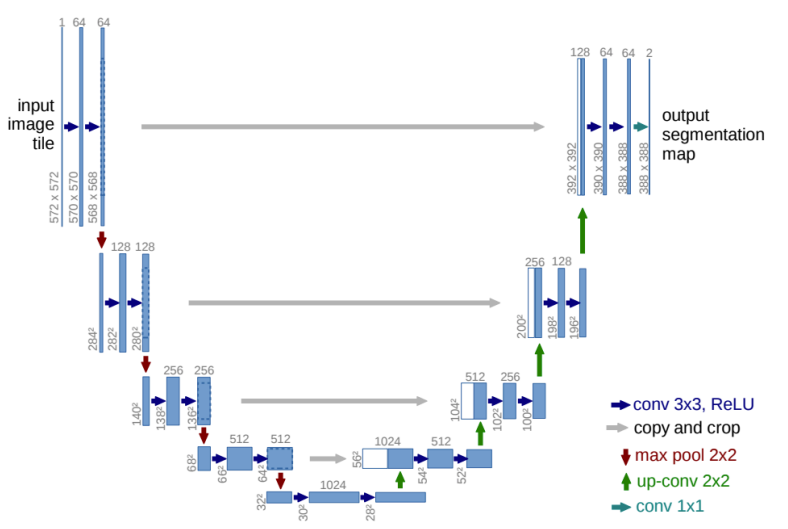
U Net
- FCN을 유사한 구조를 가진 Segmentation 모델
- Feature를 추출하는 Contracting 과정과 Upsampling을 단계적으로 진행하는 Expanding 과정으로 나뉜다
- Contracting Path
- 한번의 과정이 끝날 때 마다 Channel 수를 2배로 늘린다
- 기존의 FCN의 추출과정과 비슷하다
- Expanding Path
- 해상도를 2배씩 늘리면서 점진적으로 Upsampling을 진행한다
- 반대로 Channel수는 절반으로 줄이면서 진행한다
- Contracting 과정에서 대칭으로 대응되는 Layer에서 나온 Map과 Concatenating을 진행해서 Fusion 시킨다
- 주의할점
- MaxPooling을 통해서 크기를 반으로 점진적으로 줄이고 다시 Upsampling을 통해 2배씩 늘려나가기 때문에 이미지 사이즈가 홀수일 경우 차원이 맞지않아 계산이 불가능하다
DeepLab
- 구글에서 2018년에 작성된 논문으로 그 당시 좋은 성능을 보여주었다
- 모델의 특징으로는 Dilated convolution와 Depthwise separable convolution를 이용하여 파라미터 수를 줄이면서 성능을 유지시켰다
- 본 글에서는 논문의 주된 특징인 Dilated convolution와 Depthwise separable convolution Layer에 대해서 다룬다
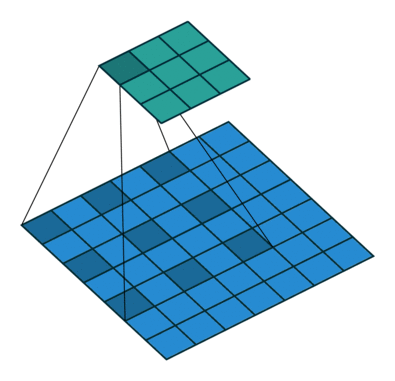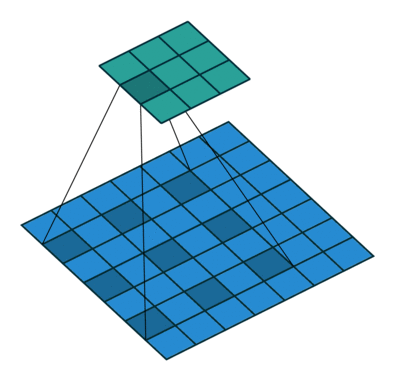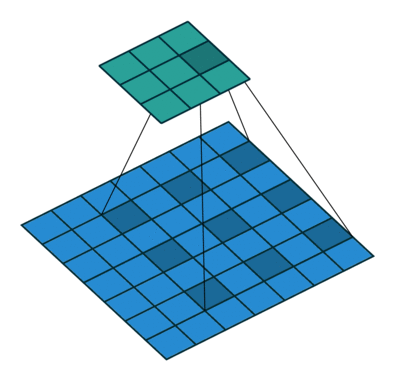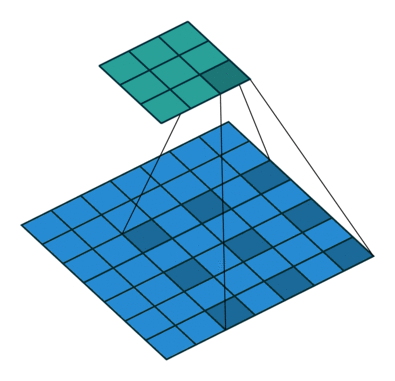
Dilated convolution
- Atrous Convolution 이라고도 한다
- 필터 내부에 빈 공간이 존재하는 Convolution Layer를 말한다
- parameter r을 조절하여 내부의 빈 공간의 크기를 조절 할 수 있다
- 1일 경우 기본적인 Convolution Layer와 동일
- 동일한 양의 파라미터와 계산량을 유지하면서 한 픽셀이 볼 수 있는 영역을 크게 할 수 있다.
- 기존에 한 픽셀이 볼 수 있는 영역을 크게 하기위해서는 Kernel Size를 키워야 했는데 이는 필연적으로 파라미터와 계산량의 증가가 따라온다
- 이미지 데이터의 경우에는 한 픽셀 주위의 픽셀이 어느정도 연관이 되어있다고 가정할 수 있기 때문에 가능한 방식으로 생각된다
Depthwise separable convolution
- 기존 Convolution Layer의 연산을 2단계로 분리시켜서 사용되는 파라미터 수를 획기적으로 줄인 방법이다
- Convolution Layer에서는 Channel축을 필터가 한번에 연산하지만, Depthwise separable convolution Layer에서는 Channel을 분리해서 1의 길이를 가지는 여러개의 Feature로 만들고 여기에 1 x 1 x 채널길의 크기의 필터를 다시한번 적용하여 연산을 하는 방식을 취한다
- 이를 통해서 기존 연산에서는 $H \times W \times C \times n$ 개의 파라미터가 필요 했지만 Depthwise separable convolution 연산에서는 $H \times W \times C + C \times n$ 개의 파라미터가 필요하게 되어 수를 더욱 줄일 수 있었다.