1. 기초과제

• 과제 내용
  • 간단한 python의 built-in function 과 문자열 처리를 위한 과제
• 결과
  • 정규식 라이브러리 re를 사용하여 문자열을 처리해주었다
• 회고
  • 기초과제 + 첫주라 그런지 난이도는 어렵지 않았다
  • 문제표현상 애매한 점이있었지만, 조교님과의 소통으로 해결함

2. 심화과제

• 여기서부터 진정한 과제

1. 경사하강법 구현

• 말 그대로 경사하강법의 구현
• 차근차근 수식을 코드로 바꾸면 되기때문에 어려운부분은 없었다

2. BPTT 구현

• 과정
  • RNN의 Backpropagation은 처음 구현하는거라 시행착오가 많았다
• numpy를 거의 사용 안하고 문제를 풀었는데 조금 연습을 할 필요가 있어보인다

3. 최대가능도 계산 증명 및 구현

• 가우시안 분포를 통한 최대가능도 계산

• 로그우도함수
  $$
  \begin{aligned}
  L(\theta|x) &= \sum_{i=1}^{n}\left( -\frac{1}{2}\log2\pi\sigma^2 +\log \exp\left(-\frac{(x_i-\mu)^2}{2\sigma^2}\right) \right)\\
  &= -\frac{n}{2}\log2\pi\sigma^2 - \sum_{i=1}^{n}\frac{(x_i-\mu)^2}{2\sigma^2}\\
  &= -\frac{n}{2}\log2\pi\sigma^2 - \frac{1}{2\sigma^2}\sum_{i=1}^{n}(x_i-\mu)^2
  \end{aligned}
  $$

• 모평균의 추정량
  $$
  \begin{aligned}
  \frac{\partial L(\theta|x)}{\partial \mu}&= -\frac{1}{2\sigma^2}\sum_{i=1}^{n}\frac{\partial}{\partial \mu}\left(x_i^2-2x_i\mu+\mu^2\right)\\
  &= -\frac{1}{2\sigma^2}\sum_{i=1}^{n}(-2x_i + 2\mu)\\
  &= \frac{X-n\mu}{\sigma^2}\\
  \hat{\mu} &= \frac{1}{n}X\\
  &= \frac{1}{n}\sum_{i=1}^{n}x_i
  \end{aligned}
  $$

• 모분산의 추정량
  $$\frac{\partial L(\theta|x)}{\partial \sigma} = -\frac{n}{\sigma} + \frac{1}{\sigma^3}\sum_{i=1}^{n}(x_i-\mu)^2$$
  $$\hat{\sigma}^2 = \frac{1}{n}\sum_{i=1}^{n}(x_i-\mu)^2$$

후기

• 우린 앞으로 편미분과 평생을 같이 살아야한다고
• 역시 스스로 힘으로 문제를 해결하면 기분이 좋다
• 다음 심화과제는 어떨지 궁금하다

오늘 하루 한 것

• 정리
  • RNN
  • 딥러닝 기초

피어세션에서 한 것

• 무어 펜로즈 역행렬 간단하게 설명하기
• 일주일 회고

주말에 할 것

• 추가 정리
  • 정규식
  • pickles
  • __init__.py, __main__.py
  • numpy, pandas 정리
  • KL diverence
  • 여러가지 활성함수

하루 느낀점

• 마지막 날이지만 주말에 정리할게 많다.

8. RNN

• 연속적인 데이터(Sequence Data)를 주로 다루는 Nerual Network
• 소리, 문자열, 주가등의 데이터를 분석하는데 사용된다

8.1 시계열 데이터

• 독립동등분포 가정을 잘 위배하기 때문에 순서를 바꾸거나 과거에 정보에 손실이 발생하면 데이터의 확률분포 자체가 변해버린다

• 베이즈 법칙을 이용하여 다음과 같이 표현이 가능하다
  $$
  \begin{aligned}
  P(X_1, … ,X_{t}) & = P(X_t|X_1, …, X{t-1})P(X_1,…,X_{t-1})\\
  & = \prod_{s=1}^{t}P(X_s|X_{s-1},…,X_1)
  \end{aligned}
  $$

• 시퀸스 데이터를 다루기 위해서는 길이가 가변적인 데이터를 다룰수 있는 모델이 필요하다

  • 조건부에 들어가는 데이터의 길이는 시퀸스마다 가변적이다
    $$
    \begin{aligned}
    X_t &\sim P(X_t|X_{t-1}, … X_{1})\\
    X_{t+1} &\sim P(X_t|X_{t}, X_{t-1}, … X_{1})
    \end{aligned}
    $$

• 고정된길이 $\tau$ 만큼의 시퀸스만 사용하는 모델의 경우 자기회귀모델(Autoregressive Model)이라고 한다

  • 매우 오래된 과거의 데이터는 실제 데이터에 큰 영향을 주기 힘들다는 가정하에 세워진 모델이다
    $$
    \begin{aligned}
    X_t &\sim P(X_t|X_{t-1}, … X_{t-\tau})\\
    X_{t+1} &\sim P(X_t|X_{t}, … X_{t-\tau+1})
    \end{aligned}
    $$

• 이전정보를 제외한 나머지 정보들을 잠재변수로 활용하는 모델을 잠재자기회귀모델 이라고 한다

  • 앞으로 다룰 RNN도 이 모델에 해당한다
    $$
    \begin{aligned}
    X_t &\sim P(X_t|X_{t-1}, H_t)\\
    X_{t+1}&\sim P(X_t|X_{t}, H_{t+1})\\
    H_t&=\operatorname{Net}(H_{t-1}, X_{t-1})
    \end{aligned}
    $$

8.2 RNN

• 기본적인 RNN 모델은 아래와 같이 MLP와 유사한 형태를 가지고 있다
• RNN은 이전순서의 잠재변수와 현재의 입렬을 활용하여 계산을 이어나간다
• RNN의 역전파는 BPTT(Backpropagation Through Time)라고 불리며 연결그래프에 따라 순차적으로 계산한다

  • $S$ : 잠재변수
  • $X$ : input Data
  • $W_x$ : $X$의 가중치행렬
  • $W_{rec}$ : $S$의 가중치 행렬
  • $\sigma$ : Activate Function
  • $X$ : 시퀸스 데이터

• RNN의 Network 연산

$$
\mathbf{S_{t}} = \sigma (\mathbf{O}_{t-1} + \mathbf{X}_{t}\mathbf{W}_{x})
$$
$$
\mathbf{O_{t}} = \mathbf{S}_{t}\mathbf{W}_{rec}
$$

• BPTT
  • RNN의 Backpropagation 을 계산해보면 미분의 곱으로 이루어진 항이 계산된다
  • 시퀸스의 길이만큼의 $W_{rec}$의 역전파가 이루어 질 때 마다 계속해서 미분을 하기 때문에 시퀸스의 길이가 길어질수록 gradient vanishing(기울기 소실)이 발생하여 계산이 불안정해 진다

    • $L$ : loss 함수
    • $y$ : target

$$
\frac{\partial S_{t}}{\partial W_{rec}} = \sum_{i=1}^{t-1} \left( \prod_{j=i+1}^{t} \frac{\partial S_{j}}{\partial S_{j-1}} \right)\frac{\partial S_{i}}{\partial W_{rec}} + \frac{\partial S_{t-1}}{\partial W_{rec}}
$$

• truncated BPTT
  • RNN은 시퀸스의 길이가 길어지면 기울기 소실이 발생하여 계산이 불안정해지기 때문에 중간에 연산을 끊어주는 테크닉.
• 이러한 기울기 소실을 해결하기 위해 등장한 네트워크
  • LSTM, GRU

6. 베이즈 통계학

• 하나의 사건에서 믿음의 정도를 확률로 나타내는 베이즈 확률론에 기반한 통계학 이론
• 쉽게 말하면 아직 일어나지 않은 사건이 일어날 확률에 대한 계산을 하는 학문

6.0 조건부 확률

• 조건부확률 $P(A|B)$
  특정사건 $B$가 일어난 상황에서 사건 $A$가 일어날 확률이다. 아래와 같이 나타낼 수 있다.

  $A$와 $B$가 동시에 일어날 확률 = $B$가 일어날 확률 * $B$일어난 상황에서 $A$가 일어날 확률
  $$
  P(A\cap B) = P(B), P(A|B) = P(A), P(B|A)
  $$
  $$
  P(B|A) = \frac{P(A\cap B)}{P(A)} = P(B) \frac{P(A|B)}{P(A)}
  $$

6.1 베이즈 정리

• $D$ : 데이터

• $\theta$ : 측정하고싶은 파라미터

• 조건부 확률 $P(\theta|D)$는 사후확률이라고 부른다

• 조건부 확률 $P(D|\theta)$는 가능도(likehood, 우도)라고 부른다

• $P(\theta)$ 는 사전확률이라고 부른다

• 베이즈 정리는 아래와 같이 나타내며 이식으로 부터 우리는 사후확률과 가능도는 비례하는 관계임을 알 수 있다
  $$
  P(\theta|D) = P(\theta) \frac{P(D|\theta)}{P(D)}
  $$

• 조건부 확률의 시각화

  • 정밀도(Precision) : 모델이 True라고 분류한 것들 중에서 실제 True인 것의 비율
  • 재현율(Recall) : 실제 True인 것 중에서 모델이 True라고 예측한 것의 비율
  • 정확도(Accuracy) : 올바르게 예측한 정도
    $$
    Precision = \frac{TP}{TP+FP}
    $$
    $$
    Recall = \frac{TP}{TP+FN}
    $$
    $$
    Accruacy = \frac{TP + TN}{TP+FN+FP+TN}
    $$

• 새로운 데이터가 들어왔을때 앞서 계산한 사후확률을 사전확률로 사용하여 새로운 사후확률로 갱신할 수 있다
  $$
  P^{\prime}(\theta|D) = P(\theta|D) \frac{P(D|\theta)}{P(D)}
  $$

• 조건부 확률은 일어나지 않은 일에 대해 유용한 통계적 해석을 제공하지만 인과관계를 추론할때는 함부로 사용해서는 안된다

• robust한 모델을 위해서는 인과관계를 생각할 필요가 있다

오늘 하루 한 것

• 강의
  • 모든강의 다 끝냄
• 과제
  • 심화과제 완료
• 정리
  • 통계학
  • 베이즈 통계학

피어세션에서 한 것

• 선형회귀 경사하강법에 대한 질문

내일 할것

• 정리 마무리!
• 과제회고
• 피어세션 질문 정리

주말에 할 것

• 추가 정리
  • 정규식
  • pickles
  • __init__.py, __main__.py
  • numpy, pandas 정리
  • KL diverence

하루 느낀점

• 생각보다 많이 정리하지는 못했다
• 제출은 안하지만 답지 받기전까지 끝내고 싶어서 심화과제에 시간을 많이 투자했다

4. 딥러닝 기본

• 딥러닝은 비선형모델인 신경망을 이용한 기계학습이다

4.1 softmax 함수

• 모델의 출력을 확률로 해석 할 수 있게 변환해주는 함수
• 인공신경망에서 확률분포를 얻기위한 마지막 활성함수로 많이 사용한다
• 출력값은 항상 0~1사이로 정규화된다
  $$
  f(x)_{k} = \frac{e^{x_i}}{\sum_{k=1}^{n}e^{x_{k}}}
  $$

4.2 Activation Function (활성함수)

• 실수범위에서 정의된 비선형 함수
• 딥러닝을 비선형 모델로 만들어주는 결정적인 함수이다
• 여러가지 종류가 있으며 ReLU계열이 제일 많이 사용되고 있다
• 포스팅을 통해 따로 다룰 예정이다

4.3 신경망

• 선형모델과 활성함수를 합성한 함수이다
• 우리가 흔히 부르는 MLP(Multi Layer Perceptron)는 여러 층의 합성신경망을 뜻한다

• $x$ : input
• $\sigma$ : Activation Function
• $h$ : Layer output
• $z$ : linear output
• $W$ : weight matrix
• $b$ : bias
  $$
  h = \sigma(z)\\
  z = Wx + b\\
  $$

4.4 Backpropagation

• MLP의 weight들을 효율적으로 갱신하는 알고리즘
• 합성함수의 미분법인 Chain-rule 기반으로 output Layer부터 input Layer로 미분을 계산해 나간다

$$
O = W_{2}h + b_{2}\\
h = \sigma(z)\\
z = W_{1}x + b_{1}\\
$$

이 글에서 미분은 다루지 않습니다

3. 경사하강법

• 함수의 극소값의 위치를 구할때 사용하는 방법
• 현재값의 기울기를 이용하여 점점 극소값에 접근한다
• 기울기가 너무 커서 발산할 경우를 방지하기 위해 lr(learning rate)를 곱해서 충분히 작은 값으로 계산을 해준다
• 컴퓨터로 계산할 경우 딱 떨어지는 정수를 만들어내기 힘들기 때문에 $\epsilon$ 값보다 작아질 경우를 수렴했다라고 가정한다

$$
x_{i+1} \leftarrow x_{i} - \gamma \nabla f(x_{i})
$$

• python code

  1 2 3 4 5

  var = init # 초기값 grad = gradient(var) # 현재 위치로부터 기울기를 구하는 함수 while (abs(grad) > eps): var += - lr * grad grad = gradient(var)

• 벡터가 입력인 다변수 함수의 경우는 편미분을 이용하여 경사하강법을 진행한다

3.1 선형회귀에서의 경사하강법

• 선형회귀에서의 target은 $\left\|\mathbf{y-X\beta}\right\|_{2}$ 이고, 이를 최소화하는 $\beta$를 찾아야 하기 때문에 아래와 같은 gradient를 구해야 한다

$$
\nabla_{\beta}\left\|\mathbf{y-X\beta}\right\|_{2}=-\frac{\mathbf{X^{\top}(y-X\beta)}}{n\left\|\mathbf{y-X\beta}\right\|_{2}}
$$

• 위의 식을 통하여 $\beta$를 구하는 경사하강법 알고리즘은 아래와 같다

$$
\begin{eqnarray*}
\beta_{i+1}&\leftarrow\beta_{i}-\gamma\nabla_{\beta}\left\|\mathbf{y-X\beta_{i}}\right\|_{2}\\
\beta_{i+1}&\leftarrow\beta_{i} + \gamma \frac{\mathbf{X^{\top}(y-X\beta)}}{n\left\|\mathbf{y-X\beta}\right\|_{2}}
\end{eqnarray*}
$$

• 간략하게 아래와 같이 표현도 가능하다
  • gradient를 최소화시키는것과 gradient의 제곱을 최소화 시키는것은 같은 의미

$$
\beta_{i+1} \leftarrow \beta_{i} + \frac{2\gamma}{n} \mathbf{X^{\top}(y-X\beta)}
$$

3.2 경사하강법의 한계

• 볼록한 함수에서는 적절한 학습률과 반복횟수를 선택했을 때 수렴이 보장되어있다
• 비선형회귀의 경우 목적식이 볼록하지 않기 때문에 수렴이 항상 보장되지는 않는다
• 특히 딥러닝의 경우 고차원의 자료를 다루기 때문에 경사하강법만으로는 학습하기가 힘들다

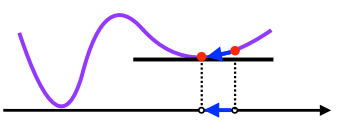
• 이러한 이유로 SGD, Momentom, Adam 등의 여러가지 optimize 알고리즘이 등장했다
• 이 부분에 대해서는 추후에 따로 다룰 예정이다

14. Exception Handing

• 사전에 인지했거나 예측 하지못한 각종의 예외들을 대처하기위한 방법
• 개발자가 반드시 명시적으로 정의해야한다
• try ~ except

1
2
3
4

try:
    예외 발생 가능 코드
except (exception 종류):
    예외 발생시 대응하는 코드

• try ~ except ~ else
  • else : 예외가 발생하지 않을때 진행하는 부분

1
2
3
4
5
6

try:
    예외 발생 가능 코드
except (exception 종류):
    예외 발생시 대응하는 코드
else:
    예외가 발생하지 않을 때 동작하는 코드

• try ~ except ~ finally
  • finally : 예외가 발생해도 진행하는 부분

1
2
3
4
5
6

try:
    예외 발생 가능 코드
except (exception 종류):
    예외 발생시 대응하는 코드
finally:
    예외에 상관없이 동작하는 코드

• 기본적으로 제공하는 exception 종류 : 링크
• raise 함수를 사용하여 강제로 Error나 Exception을 발생시킬 수 있다.

15. File Handing

• 코드로 파일을 처리하기 위한 방법
• 파일 처리를 위해서 open 을 사용한다

  1 2 3 4

  f = open('파일이름', '접근모드') ... ... f.close()

  모드	설명
  r	읽기모드 - 파일 내용을 읽어올 때 사용
  w	쓰기모드 - 파일 내용을 수정할 때 사용
  a	추가모드 - 파일에 내용을 추가할 때 사용
  b	바이너리 모드 - 바이너리형식으로 파일을 읽기/수정/추가할 때 사용
  +	파일을 읽고 쓰기용으로 열기 (앞의 모드에 따라서 파일 포인터의 위치차이가 존재한다)
  x	쓰기모드로 생성하는데 이미 파일이 존재할 경우 예외를 발생시킨다

16. Logging Handling

• Log
  프로그램이 실행되는 동안 일어 나는 정보를 말한다. 이런 기록들을 모아 분석하여 의미있는 결과를 도출 할 수 있기 때문에 Log를 따로 관리하는 모듈을 사용한다
• Python의 기본 Log 관리모듈 logging이 존재한다
• logging level에 관련한 표 : 아래로 내려갈수록 높은 레벨의 log이다

12. Module 모듈

• 작은 프로그램 조각
  이 조각들을 모아서 하나의 큰 프로그램을 만든다
• 사용하는 이유 : 다른 프로그램에서 사용하기가 편하다
  편하면 무조건 해야지
• module == .py 파일
• import 문을 사용하여 같은폴더 내의 module 이나 package를 호출한다
• module을 호출하는 방법
  1. 별칭으로 호출
  2. 특정 함수 또는 클래스만 호출
  3. 모듈에 모든 함수또는 클래스를 호출

1
2
3

import numpy as np  # 1
from numpy import ndarray  # 2
from numpy import *  # 3

• python에는 수많은 Built-in Modules이 존재한다
  • random, tqdm, time, collection, heap, Math …

13. package

• 다양한 모듈이 모여서 이루어진 코드 묶음
• 오픈소스들이 모두 패키지로 관리된다
• 각 폴더별로 필요한 모듈을 구현하고, __init__.py를 구성한다
• 추후에 __init__.py 와 __main__.py 작성법에 관련되어 포스팅을 할 예정이다

Peer Session 정리

• 일주일동안 피어세션에서 주고받았던 질문에 대해서 추려서 정리한 글이다

1. python 메모리 관리는 어떤 방식으로 이루어지나?

• 영상참조하면 좋을것 같다
  • https://www.youtube.com/watch?v=arxWaw-E8QQ

2. list 구조체의 메모리는 어떤방식으로 할당 될까

• python의 list는 다른 언어의 array와 다르게 list 내부에 여러가지 데이터 형식이 들어가는 것이 가능하다
  • linked list 형태로 data가 추가 될 때마다 그 형식에 맞는 메모리를 할당해서 연결하기 때문에 가능하다

3. python float의 할당 방식은 어떻게 이루어 질까? + int 형과의 비교

• python의 float 형은 64bit의 부동소수점으로 표현을 한다
• 기억 범위 : $4.9×10^{-324}\sim1.8×10^{308}$
• 부동소수점 표현
  • 부호, 지수비트, 가수비트로 나눠서 수를 표현하는 방식을 말한다
  • 자세한 설명은 따로 포스팅 할 예정이다

3.1 python에서 int형의 범위는 어떻게 될까

• python3 버전으로 넘어오면서 int형의 overflow가 사라졌다
• 그래서 int형으로 표현할 수 있는 범위는 메모리가 허용하는 한도내에서 무제한이다
• 조금더 자세하게 설명하자면 python2 버전에서는 int와 long 타입을 같이 사용하는 구조였는데 int의 범위가 넘어가면 자동으로 long 타입으로 넘어가는 형식이었다.
• python3에서는 아에 long 타입이 int와 결합해서 수의 크기에 따라 탄력적으로 가용메모리를 추가적으로 할당하는 Arbitrary presicion을 사용한다