---

Missingno

• 결측치를 시각화 해주는 라이브러리
• 빠르게 결측치의 분포를 확인할 때 사용가능하다
• missingno library를 사용한다

plotly

• interactive한 시각화를 할때 사용하는 시각화 라이브러리
• 추가적으로 다룰 예정이다
• Treemap같은 계층을 interactive 하게 보여줄때 사용한다

Waffle Chart

• pywaffle
• 와플형태로 discrete하게 값을 나타내는 차트
  • github commit형태
• icon을 이용해서 표현을 할 수 있다
• info graphic 에 유용하게 사용가능하다

Venn

• 집합으로 표현하는 시각화
• pyvenn을 사용
• EDA보다는 출판용으로 사용하는것이 좋다
  • 가독성이 좋지 않다

reference

• Naver Connect Boostcamp - ai tech

---

1. 오늘 하루 한 것

• 정리
  • LSTM 마무리
• 과제
  • 심화과제
• GAN에 관한 추가 내용 공부

2. 피어세션에서 한 것

• pixelRNN 관련한 글

3. 내일 할 것

• VAE 추가공부, Data 시각화 마무리

4. 하루 느낀점

• 예전에 간단하게 정리해 두었던 GAN을 보니 기억이 새록새록 떠오른다

---

1. 오늘 하루 한 것

• 강의
  • Generative Model
• 과제
  • 심화과제
• SSD 논문리딩

2. 피어세션에서 한 것

• 각종 Attention에 관한 이야기

3. 내일 할 것

• 강의 정리, 논문 정리, 스몰톡 주제 정리

4. 하루 느낀점

• 모더레이터….

---

GAN

• 적대적 생성모델
• 노이즈로부터 데이터를 생성하는 Generator와 데이터가 진짜 데이터인지 생성된 데이터인지를 판단하는 Discriminator 2개의 구조로 이루어져 있다
• Generator와 Discriminator는 서로의 Loss값을 최대로 하는 방향으로 학습을 하려 한다
  • Generator는 Discriminator의 판단한 결과로 실제 데이터와 유사하게 학습하는 방향으로 학습한다
  • Discriminator는 이진분류기로 실제데이터와 생성데이터를 분류한다

• GAN을 아래와 같이 표현이 가능하다.
  $$
  min_G, max_D, V(D,G) = \mathbf{E}{x\sim p{data}(x)}[\operatorname{log}D(x)] + \mathbf{E}{z \sim p{z}(z)}[\operatorname{log}(1 - D(G(z)))]
  $$

GAN & VAE

• VAE
  • 학습이 안정적이다
  • 결과물이 흐릿하게 나올 확률이 높다
  • 학습 데이터에 있는 데이터와 비슷하게 나온다
    • 새로운것을 만들어내지는 못함
• GAN
  • 학습이 불안전하다
  • 출력물이 뚜렷한 편이다
    • 새로운 분포를 만들 수 있다
• 최근에는 VAE또한 많이 발전해서 output이 GAN 이상의 것들을 보여준다

  reference

• Naver Connect Boostcamp - ai tech

---

Generative Model

• 생성모델은 아래와 같은 특징을 가진다
• Generatation
  • 기존의 데이터 확률분포 $p(x)$ 에 속하는 $x_new$를 만들어 낸다
• Density estimation
  • data $x$가 기존의 데이터와 비슷하면 확률분포 $p(x)$상에 존재할 가능성이 높다.
  • anomaly detection 이상치 탐지
  • 설명 가능한 모델 등이 있다

Variaty Autoencoder

• Latent Space로 부터 데이터를 생성해내는 모델을 말한다
• Encoder와 Decoder 2부분으로 이루어져 있다
  • Encoder에서는 기존의 Dataset으로 부터 Latent Space를 생성한다
    • $x \rightarrow p(x)$
  • Decoder는 Latent Space로부터 역으로 Data를 생성한다
    • $p(x) \rightarrow x$
• 그래서 Encoder에서는 Dataset으로 Latent Space의 확률분포를 근사하고
  • $q_\phi$(z|x)
• Decoder에서는 Latent Space에서 기존 Dataset의 확률분포로 이동을 시켜준다
  • $p_\theta(x)$
  • 하지만 위의 확률분포는 우리가 알 방법이 없다
• 그래서 이것을 근사하기 위해 VAE에서 사용된 2가지 기법에 대해서 간략하게 설명한다

Variaty Inference

• $q_\phi(z|x)$와 $p_\theta(z|x)$의 차이($D_{KL}$)를 줄이는것이 궁극적인 목표이다

  • 하지만 $p_\theta(z|x)$은 우리가 알 수가 없다

• 그래서 Maximum Likehood를 변형시켜서 학습에 이용한다

• $\mathcal{L}(\theta, \phi ; x)$ : Evidence Lower Bound (ELBO)
  $$
  \begin{aligned}
  log(p_\theta (x)) &= \int_z q_\phi(z|x)log(p_\theta(x))\\
  &= \mathcal{L}(\theta, \phi ; x) + D_{KL}(q_\phi(z|x)||p_\theta(z|x))
  \end{aligned}
  $$

• $D_{KL}$는 항상 1보다 크기때문에 위의 식은 다음과 같이 나타낼 수 있다.

$$
log(p_\theta (x)) \geq \mathcal{L}(\theta, \phi ; x)
$$

• 여기서 ELBO를 크게 하는 쪽으로 학습을 하게되면 $D_{KL}$은 줄어들게 된다.

Reparametrization Trick

• 학습과정 중간에 Sampling이 들어가서 미분이 되지 않는것을 해결하기 위한 Trick
• sampling 한 값 $z$가 $\mu_q + \sigma_q \cdot \epsilon$ 과 같다고 생각하고 기존에 없던 $z$에 대해서 미분이 가능하게 바꾸었다.

reference

• Naver Connect Boostcamp - ai tech
• PR-[010] : Auto-Encoding variational Bayes ICLR 2014
• VARIATIONAL-AUTOENCODER와 ELBO(EVIDENCE LOWER BOUND)

---

Sequential Model

Naive sequeance model

• 과거 모든시점의 데이터를 고려해야한다
• 시퀸스가 진행될 수록 고려해야할 데이터 양이 늘어남

Autoregressive model

• 특정 과거 시점 이후의 데이터만 고려한다

  Markov model

• Markov Chain role에 의하여 바로 전 state가 이전시점의 모든 데이터를 가지고 있다고 가정한다
• 위의 이유로 바로 전 시점의 데이터만 고려함
• 강화학습에서 많이 사용하는데 현실에 직접 적용하기에는 버려지는 정보량이 너무 많다

Latent autoregressive model

• 과거의 모든 정보들을 요약한 hidden state를 사용한다
  • hidden state가 어떻게 정의되느냐에 따라서 모델간 많은 차이가 존재한다
• RNN도 Latent autoregressive model라고 볼 수 있다

---

Recurrent Neural Network (RNN)

• 자기참조로 학습하는 네트워크

• short-term dependencies
  • 먼 과거의 정보(Long-term)는 고려하기 힘들다
  • 자기참조로 인한 연산이 계속되면서 gradient vanishing(sigmoid, tanh)이나 exploring(ReLU 계열)이 발생한다

Long Short Term Memory

• 먼 과거의 정보를 고려하기위해 고안된 RNN

• 기존에 존재하는 Hidden state에 내부에서만 연산되는 Cell State를 추가하여 먼 과거의 정보 또한 잘 기억할 수 있다

• $x$ : data

• $C$ : Cell state

• $h$ : hidden state

• $\sigma$ : sigmoid function

• $tanh$ : hyperbolic tan function

Cell state

• 먼 과거의 정보까지 요약해서 가지고 있다가 Hidden state에 넘겨주는 역할
• 과거의 정보가 희석되는것을 막는 Resnet의 Skip Connection과 비슷한 역할을 한다
• Cell state는 다음과 같은 과정으로 업데이트 된다

1. $t-1$시점의 Hidden state가 Forget Gate를 통과
   • Forget Gate : 중요하지 않은 정보들을 없애는 Gate
     $$
     f_{t} = \sigma(W_{f}\cdot[h_{t-1}, x_{t}] + b_f)
     $$
2. $t-1$시점의 Hidden state가 Input Gate를 통과
   • Input Gate : Cell state에 저장해야하는 정보들을 결정하는 Gate
     $$
     \begin{aligned}
     i_{t} &= \sigma(W_{i}\centerdot [h_{t-1}, x_{t}] + b_{f})\\
     \tilde{C_{t}} &= tanh(W_{C}\cdot [h_{t-1}, x_{t} ]+b_{C})
     \end{aligned}
     $$
3. $t-1$시점의 Cell state와 Gate를 통해서 나온 값들의 연산으로 Cell state를 업데이트 한다
   $$
   C_{t} = f_{t} * C_{t-1} + i_{t}*\tilde{C_{t}}
   $$

Hidden state

• 기존의 RNN에 Hidden state와 동일한 역할
• 아래의 Output Gate에 Cell state와 Hidden state의 연산으로 업데이트 된다

1. Output Gate
   $$
   o_t = \sigma(W_o [h_{t-1}, x_t] + b_i)\\
   h_t = o_t * tanh(C_t)
   $$

Gated Recurrent Unit (GRU)

• LSTM과 비슷한 형태
• 2개의 Gate(reset Gate, update Gate)가 존재하고 Cell state가 없다
• LSTM보다 더 적은 parameter를 가진다

reference

• Naver Connect Boostcamp - ai tech
• colah.github.io - RNN image

---

1. 오늘 하루 한 것

• 강의
  • CNN 4~6강, RNN 7강
• 정리
  • CNN 4~6강, RNN 7강
• 과제
  • CNN, RNN LSTM

2. 피어세션에서 한 것

• Batch norm weight 초기화에 관해서

3. 내일 할 것

• RNN 마무리, 논문리뷰 정리

4. 하루 느낀점

• 프로젝트 아이디어에 대해서 생각을 하는중이다 괜찮은게 있으려나?

---

Fully Convolutional Network

• CNN에서 마지막을 담당하던 Dense Layer를 Dense Layer Feature와 동일한 Channel수를 가진 Convolution Layer로 대체한 Network
• Dense Layer는 reshape을 통해서 input을 집어넣기 때문에 정해진 input size가 필요 했지만, convolution Layer의 경우 channel 이외에는 가변적이기 때문에 이미지의 크기와 상관없이 연산이 가능해졌다
• 연산을 할 때 마다 차원이 축소되는 문제가 있다 -> upsampling기법을 사용
  • conv transpose -> checker board
  • unpooling

Object Detection

R-CNN 계열

• R-CNN
  • Selective Search 로 BBox 2000개정도를 추출 한 뒤 각각 CNN을 돌린다
  • CNN 연산이 2000번 반복되기 때문에 매우 느린 속도이다
• fast R-CNN
  • SPP Net을 이용하여 기존 2000번 반복된 연산을 1번으로 줄임
• Faster R-CNN
  • Selective Search를 Region Proposal Network로 바꾼 R-CNN
  • Region Proposal Network : BBox도 네트워크 학습으로 뽑아내자
  • 기존에 존재하는 anchor Box(샘플한 여러 크기의 Bbox)와 이미지를 비교하여 물체가 있을법한 장소를 탐색하고, 대략적인 Bbox위치를 특정한다

Yolo

• BBox와 Classfication이 동시에 이루어지는 1 stage 모델
• R-CNN 계열에 비해서 속도가 매우 빠르지만, 정확도는 조금 떨어진다
• 실시간 물체검출이나 추적에 용이한 모델이다

reference

• Naver Connect Boostcamp - ai tech

---

AlexNet

• CNN으로 구성된 Network
• 시작부분에 11 x 11의 큰 convolution Layer를 사용했다

VGGNet

• 여러장의 3 x 3의 convolution Layer와 2 x 2 MaxPooling을 사용하였다
• 여러장의 3 x 3의 convolution Layer를 사용하면서 다음과 같은 advantage를 얻었다
  • 큰 convolution Layer와 동일한 연산을 더 작은 Parameter로 수행할 수 있다
  • receptive field를 크게 유지할 수 있다
  • 더 깊게 비선형적으로 Layer 추가가 가능해 진다

GoogLeNet

• 1 x 1, 3 x 3, 5 x 5, maxpooling을 이용하여 inception module을 구성하였다
• 1 x 1 convolution Layer를 이용해서 Channel 수를 줄여주었다

• Layer가 깊어지면서 Gradient Vanashing이 일어나는것을 막기위해 Auxiliary classifier를 두어서 추가적으로 Gradient를 더해주었다
  • inference시에는 사용되지 않는다

ResNet

• Skip Conncetion을 두어 Gradient Vanashing을 해결하여 더 많게 레이어를 쌓은 모델이다
• VGGnet의 3x3을 차용하여 파라미터 수를 크게 늘리지 않으면서 레이어를 더 쌓았다
• channel이 변하는 구간에서는 DownSampling을 통하여 channel과 Height, weight를 맞춰주었다

reference

• Naver Connect Boostcamp - ai tech

---

Convolution Neural Network (CNN)

• 시각적 데이터르 분석하는데 사용되는 인공신경망
• CNN은 크게 Convolution Layer, Pooling Layer, (Fully Cunnect Layer)로 구성된다

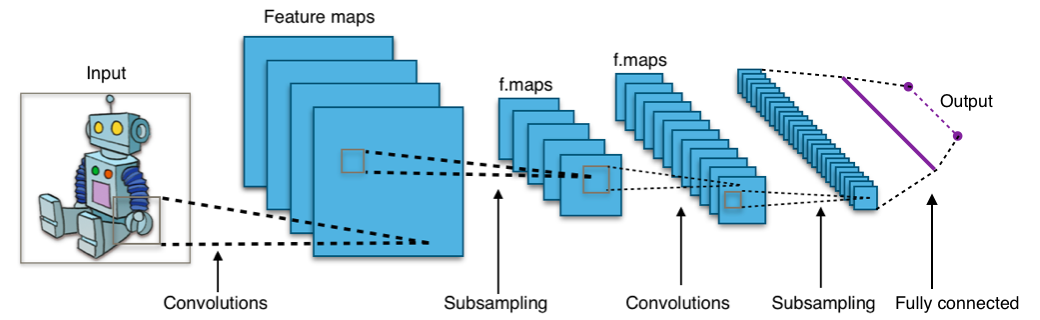
Convolution layer

• 합성곱 연산이 진행되는 레이어
• parameter의 수는 $kernel_size \times Channel_in \times Channel_out$으로 계산된다
• 이미지 처리를 할 시에 Fully Connected Layer보다 parameter 수가 월등하게 적다
• 실제 연산 이미지

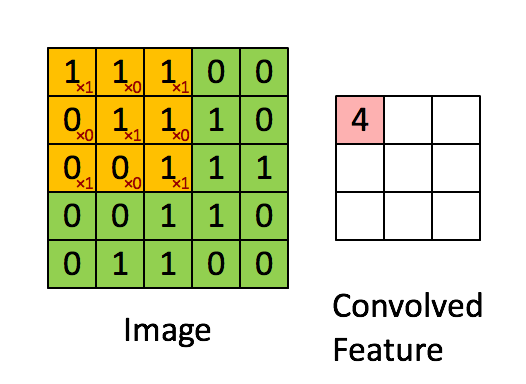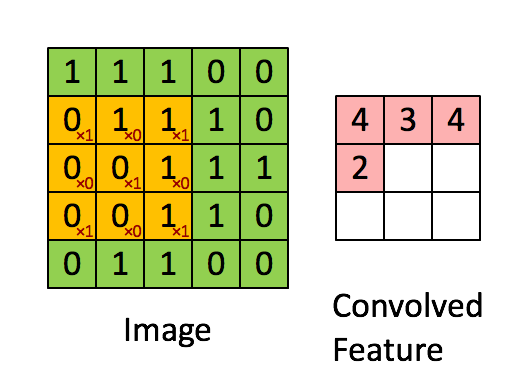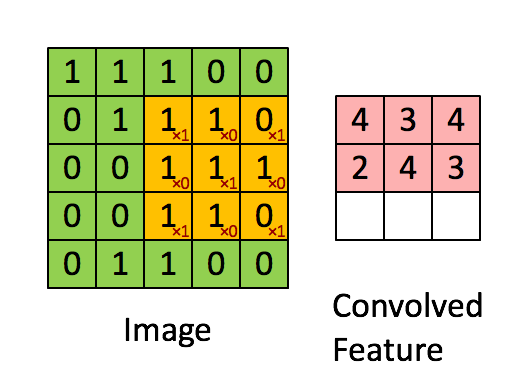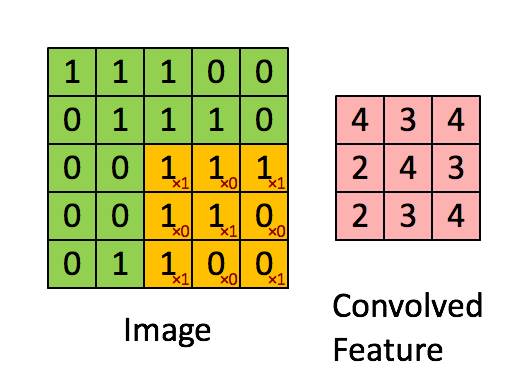
• input과 output의 크기는 아래와 같이 계산된다
• input : $(N, C_{in}, H_{in}, W_{in})$
• output : $(N, C_{out}, H_{out}, W_{out})$
• stride : 연산이 이루어지는 간격
• padding : 차원을 확장시켜 convolution 연산후에도 크기가 일정하게 유지되도록 한다
• kernel : convolution 연산을 하는 주체, filter이기도 하다
• N : batch size
• C : Channel 수
• W : 연산될 Matrix의 가로 길이
• H : 연산될 Matrix의 세로 길이

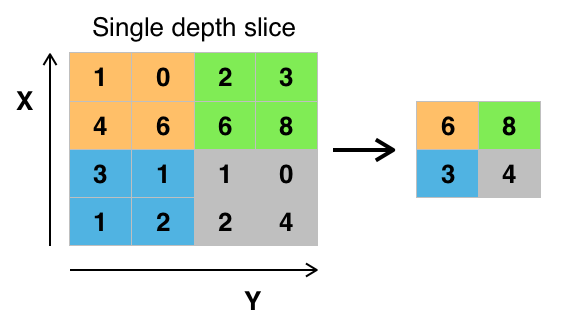
Pooling Layer

• 일정 범위안의 값들을 대표하는 하나의 값으로 압축하는 down sampling 기법
• W와 H을 줄여서 차원을 축소하고, 연산에 필요한 parameter 수를 줄인다.

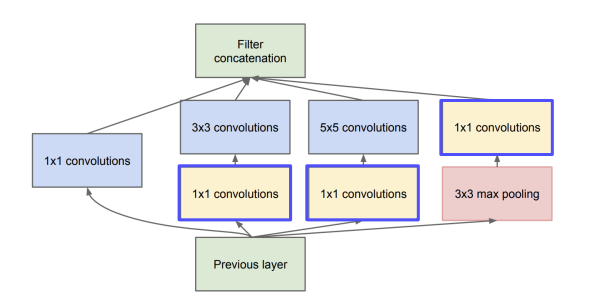
1x1 Convolution

• kernel size가 1,1인 convolution 연산을 하는것
• input, output의 W, H는 일정하지만 channel수가 감소한다.
• WHY?
  • channel 수를 줄여서 차원축소를 시키고, 추후에 연산에 필요한 parameter 수를 줄인다

$$
H_{out} = \left[ \frac{H_{in} + 2 \times \operatorname{padding[0]} - \operatorname{kernel_size[0]}}{\operatorname{stride}[0]} +1 \right]
$$

$$
W_{out} = \left[ \frac{W_{in} + 2 \times \operatorname{padding[1]} - \operatorname{kernel_size[1]}}{\operatorname{stride}[1]} +1 \right]
$$

reference

• Naver Connect Boostcamp - ai tech
• [By Aphex34 - Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=45679374]